Write equations of all tangents to the function graphics. Tangent to graphics function at point

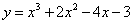
Tangency is straight That concerns the graph of the function at one point and all points of which are at the lowest distance from the graph of the function. Therefore, the tangent passes regarding the graph of the function at a certain angle and cannot pass through the touch point somewhat tangent at different angles. The equations of the tangent and equation of the normal to the graph of the function are compiled using a derivative.

The equation of tangent is derived from the equation direct .

We derive the equation of tangential, and then the equation of normal to the graph of the function.

y. = kX. + b. .

In him k. - angular coefficient.

From here we get the following entry:

y. - y.0 = k.(x. - x.0 ) .

The value of the derivative f. "(x.0 ) Functions y. = f.(x.) At point x.0 equal to the angular coefficient k. \u003d TG. φ tangent to graphics function spent through a point M.0 (x.0 , y.0 ) where y.0 = f.(x.0 ) . This is consisting geometric meaning of the derivative .

Thus, we can replace k. on the f. "(x.0 ) and get the following equation tangent to graphics function :

y. - y.0 = f. "(x.0 )(x. - x.0 ) .

In the tasks for the compilation of the equation of tangent to the graph of a function (and we will turn to them soon) the equation obtained according to the above formula equation directly in general form . To do this, all letters and numbers are transferred to the left part of the equation, and to leave zero on the right side.

Now about the equation of normal. Normal - This is a direct, passing through the touch point to the graph of the function perpendicular to the tangent. Equation Normal :

(x. - x.0 ) + f. "(x.0 )(y. - y.0 ) = 0

For warm-up, the first example is solved by independently, and then see the solution. There is every reason to hope that for our readers this task will not be a "cold shower".

Example 0. Make the equation of tangent and equation of normal to the graph of the function at the point M. (1, 1) .

Example 1. Make the equation of tangent and equation of normal to graphics function If the abscissa point of touch.

Find a derivative function:

Now we have everything you need to substitute the entry in theoretical help to obtain the equation of tangent. Receive

In this example, we were lucky: an angular coefficient turned out to be equal to zero, therefore, the equation to the general type was not needed separately. Now we can compile the equation of normal:

In the figure below: the graph of the burgundy color function, tangent of green color, orange normal normal.

The following example is also not complicated: the function, as in the previous one, is also a polynomial, but the angular coefficient will not be zero, so one more step will be added - bringing the equation to the general type.

Example 2.

Decision. Find the king point ordinate:

Find a derivative function:

.

Find the value of the derivative at the point of the touch, that is, the angular coefficient of tangent:

We substitute all the data obtained in the Formula-Dwarf and we obtain the equation of tangent:

We present the equation to the general type (all letters and numbers other than zero, we collect on the left side, and in the right leave zero):

Make an equation of normal:

Example 3. Make the equation of tangential and the equation of normal to the graph of the function, if the abscissa point of the touch.

Decision. Find the king point ordinate:

Find a derivative function:

.

Find the value of the derivative at the point of the touch, that is, the angular coefficient of tangent:

.

Find equation tangent:

Before bringing the equation to the general mind, it is necessary to "combat" a little: multiply by 4. We do this and give the equation to the general mind:

Make an equation of normal:

Example 4. Make the equation of tangential and the equation of normal to the graph of the function, if the abscissa point of the touch.

Decision. Find the king point ordinate:

.

Find a derivative function:

Find the value of the derivative at the point of the touch, that is, the angular coefficient of tangent:

.

We obtain the equation of tangent:

Give the equation to the general mind:

Make an equation of normal:

A common error in the preparation of equations of tangent and normal is not to notice that the function given in the example is complex and calculated its derivative as a different function derivative. The following examples are already with complex functions (The corresponding lesson opens in a new window).

Example 5. Make the equation of tangential and the equation of normal to the graph of the function, if the abscissa point of the touch.

Decision. Find the king point ordinate:

Attention! This function is complicated, since the Tangent argument (2 x. ) It is a function itself. Therefore, we find a derivative function as a derivative of a complex function.

At the present stage of development of education as one of its main tasks, the formation of a creative thinking personality. The ability to creativity in students can be developed only under the condition of systematic involvement of them to the basics of research activities. The foundation for applying students of his creative forces, abilities and tanks is the formed full-fledged knowledge and skills. In this regard, the problem of the formation of a system of basic knowledge and skills on each topic of the school course of mathematics has an important meaning. At the same time, full skills should be the didactic goal of non-individual tasks, but a carefully thought-out of their system. In the broadest sense, the system means a combination of interrelated interacting elements with integrity and sustainable structure.

Consider the methodology for learning students to compile an equation tangent to the function of function. Essentially, all the tasks of finding the equation of the tangent are reduced to the need to select from a set (beam, family) of direct those that satisfy certain requirements - are tangent to the graphics of some function. At the same time, a plurality of direct, from which the selection is carried out can be set in two ways:

a) point lying on the Xoy plane (central punch of direct);
b) an angular coefficient (parallel bunch of direct).

In this regard, when studying the topic "Tangential to the graph of a function" in order to deduct the elements of the system, we highlighted two types of tasks:

1) Tasks for a tangent specified point through which it passes;
2) Tasks for a tangent specified by its angular coefficient.

Training to solve the tasks for tangent was carried out with the help of an algorithm proposed by A.G. Mordkovich. Its fundamental difference from already known is that the abscissa of the touchpoint is indicated by the letter A (instead of X0), and therefore the equation of the tangent acquires the view

y \u003d f (a) + f "(a) (x - a)

(Compare with y \u003d f (x 0) + f "(x 0) (x - x 0)). This methodological technique, in our opinion, allows students faster and easier to realize where in the overall equation of tangent records of the current point coordinates, And where are the touch points.

Algorithm forcing the equation tangent to graphics of the function y \u003d f (x)

1. Given the letter A to the abscissa of the touch point.
2. Find F (A).
3. Find F "(X) and F" (a).
4. Substitute the numbers found a, f (a), f "(a) in the general equation of tangent y \u003d f (a) \u003d f" (a) (x - a).

This algorithm can be compiled on the basis of independent allocation of operations and the sequence of their implementation.

Practice has shown that the consistent solution of each of the key tasks using the algorithm allows you to form the skills of writing the equation of tangent to the graphics of the function in stages, and the steps of the algorithm serve as supporting points of action. This approach complies with the theory of phased formation of mental actions developed by P.Ya. Halperin and N.F. Talisina.

In the first type of tasks, two key tasks were allocated:

• tangent passes through a point lying on the curve (task 1);
• the tangent passes through a point that is not lying on the curve (task 2).

Task 1. Make an equation tangent to function graphics At point M (3; - 2).

Decision. Point M (3; - 2) is a point of touch, since

1. A \u003d 3 - the abscissa point of touch.
2. F (3) \u003d - 2.
3. F "(x) \u003d x 2 - 4, f" (3) \u003d 5.
y \u003d - 2 + 5 (x - 3), y \u003d 5x - 17 - equation of tangential.

Task 2. Write the equations of all tangents to the graph of the function y \u003d - x 2 - 4x + 2, passing through the point M (- 3; 6).

Decision. Point M (- 3; 6) is not a point of touch, since f (- 3) 6 (Fig. 2).

2. F (a) \u003d - a 2 - 4a + 2.
3. F "(x) \u003d - 2x - 4, f" (a) \u003d - 2a - 4.
4. Y \u003d - A 2 - 4A + 2 - 2 (A + 2) (X - A) - equation of tangent.

The tangent passes through the point M (- 3; 6), therefore, its coordinates satisfy the equation tangential.

6 \u003d - a 2 - 4a + 2 - 2 (a + 2) (- 3 - a),
A 2 + 6A + 8 \u003d 0 ^ a 1 \u003d - 4, a 2 \u003d - 2.

If a \u003d - 4, the tangent equation has the form y \u003d 4x + 18.

If a \u003d - 2, the equation of tangent has the form y \u003d 6.

In the second type, the key tasks will be the following:

• tangential parallel to some straight line (task 3);
• the tangent passes at a certain angle to this direct (task 4).

Task 3. Write the equations of all tangents to the function of the function y \u003d x 3 - 3x 2 + 3, parallel to the direct y \u003d 9x + 1.

1. A is the abscissa point of touch.
2. f (a) \u003d a 3 - 3a 2 + 3.
3. F "(X) \u003d 3X 2 - 6X, F" (A) \u003d 3A 2 - 6A.

But, on the other hand, f "(a) \u003d 9 (condition of parallelism). So it is necessary to solve the equation 3a 2 - 6a \u003d 9. Its roots a \u003d - 1, a \u003d 3 (Fig. 3).

4. 1) a \u003d - 1;
2) f (- 1) \u003d - 1;
3) f "(- 1) \u003d 9;
4) y \u003d - 1 + 9 (x + 1);

y \u003d 9x + 8 - equation of tangent;

1) a \u003d 3;
2) f (3) \u003d 3;
3) f "(3) \u003d 9;
4) y \u003d 3 + 9 (x - 3);

y \u003d 9x - 24 - equation of tangent.

Task 4. Write the equation tangent to the graph of the function y \u003d 0.5x 2 - 3x + 1, passing at an angle of 45 ° to a straight y \u003d 0 (Fig. 4).

Decision. From the condition f "(a) \u003d Tg 45 ° we find a: a - 3 \u003d 1 ^ a \u003d 4.

1. A \u003d 4 - the abscissa point of touch.
2. F (4) \u003d 8 - 12 + 1 \u003d - 3.
3. F "(4) \u003d 4 - 3 \u003d 1.
4. Y \u003d - 3 + 1 (X - 4).

y \u003d X - 7 - equation of tangential.

It is easy to show that the solution of any other task is reduced to solving one or more key tasks. Consider the following two tasks as an example.

1. Write equations of tangent to parabole Y \u003d 2X 2 - 5X - 2, if the tangents intersect at right angles and one of them concerns the parabola at the point with abscissa 3 (Fig. 5).

Decision. Since the abscissa of the touchpoint is given, then the first part of the solution is reduced to the key task 1.

1. A \u003d 3 - the abscissa point of the touch of one side of the direct angle.
2. f (3) \u003d 1.
3. F "(x) \u003d 4x - 5, f" (3) \u003d 7.
4. Y \u003d 1 + 7 (x - 3), y \u003d 7x - 20 - the first tangenecy equation.

Let A be the angle of inclination of the first tangent. Since tangents are perpendicular, then the angle of inclination of the second tangent. From the Y \u003d 7X - 20 equation, we have TG a \u003d 7. We will find

This means that the angular coefficient of the second tangent is equal.

A further solution is reduced to the key task 3.

Let B (C; F (C)) there is a point of touch the second straight, then

1. - The abscissa of the second touch point.
2.
3.
4.
- The equation of the second tangent.

Note. The angular coefficient of tangent can be found easier if the student is known as the ratio of the coefficients perpendicular direct k 1 k 2 \u003d - 1.

2. Write the equations of all common tangents to the schedules of functions.

Decision. The task is reduced to finding the abscissa of the dial points of the total tangent, that is, to solving the key problem 1 in general, the preparation of the system of equations and its subsequent solution (Fig. 6).

1. Let A be the abscissa of the touch point lying on the graph of the function y \u003d x 2 + x + 1.
2. f (a) \u003d a 2 + a + 1.
3. F "(a) \u003d 2a + 1.
4. Y \u003d a 2 + a + 1 + (2a + 1) (x - a) \u003d (2a + 1) x + 1 - a 2.

1. Let C be the abscissa of the touch point lying on the function graph
2.
3. F "(C) \u003d C.
4.

As tangent common, then

So, y \u003d x + 1 and y \u003d - 3x - 3 are common tangents.

The main objective of the considered tasks is to prepare students to independently recognize the type of key task when solving more complex tasks requiring certain research skills (ability to analyze, compare, summarize, put forward the hypothesis, etc.). Such tasks include any task in which the key task is included as a component. Consider as an example, the task (inverse problem 1) to find a function by the family of tangent.

3. At what b and c straight y \u003d x and y \u003d - 2x are tangent to graphics of the function y \u003d x 2 + bx + c?

Let T be - the abscissa of the point of touch straight y \u003d x with a parabola y \u003d x 2 + bx + c; P is the abscissa point of touch direct y \u003d - 2x with parabola y \u003d x 2 + bx + c. Then the equation of tangent y \u003d x will take the form y \u003d (2t + b) X + C - T 2, and the equation of tangent Y \u003d - 2X will take the form y \u003d (2p + b) x + c - p 2.

We will also decide the system of equations

Answer:

The article provides a detailed explanation of the definitions, the geometrical meaning of the derivative with graphic notation. The equation of tangent direct will be considered with the conversion of examples, the equations tangent to curve 2 were found.

Yandex.rtb R-A-339285-1 Definition 1

The angle of inclination direct y \u003d k X + B is called an angle α, which is counted from the positive direction of the axis about x to a straight y \u003d k x + b in the positive direction.

In the figure, the direction of X is denoted by the green arrow and in the form of a green arc, and the angle of inclination with the help of a red arc. The blue line refers to a straight line.

Definition 2.

The angular coefficient of direct y \u003d k x + B is called the numerical coefficient k.

The angular coefficient is equal to the tilt tilt straight, in other words k \u003d t G α.

• The angle of inclination is equal to 0 only with parallelism of x and an angular coefficient equal to zero, because zero tangent is 0. So, the type of equation will be y \u003d b.
• If the angle of the straight line y \u003d k x + b is sharp, then conditions are satisfied 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0, and there is an increase in the graph.
• If α \u003d π 2, then the location of the straight perpendicular about x. Equality is set using the equality x \u003d c with the value of a valid number.
• If the angle of inclination is straight y \u003d k x + b stupid, then corresponds to the conditions π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Definition 3.

The sequential is called direct, which passes through 2 points of the function F (X). In other words, the sequential is direct, which is carried out through any two points of the graph of a given function.

Figure shows that a in is the unit, and f (x) is a black curve, α - red arc, meaning the angle of inclination of the section.

When the corner coefficient is equal to the tangent of the angle of inclination, it can be seen that the tangent from the rectangular triangle A in C can be found in relation to the opposite category to the adjacent one.

Definition 4.

We get a formula for finding a securing look:

k \u003d tg α \u003d bcac \u003d f (x b) - fx a x b - x a, where the abscissions of points A and B are the values \u200b\u200bx a, x b, and f (x a), f (x b) are values Functions at these points.

Obviously, the angular coefficient of the section is determined by the equality k \u003d f (x b) - f (x a) x b - x a or k \u003d f (x a) - f (x b) x a - x b, and the equation It is necessary to write as y \u003d f (x b) - f (x a) x b - x a · x - x a + f (x a) or
y \u003d f (x a) - f (x b) x a - x b · x - x b + f (x b).

The sequential divides the graph visually to 3 parts: to the left of the point A, from A to B, to the right of V. On the figure below, the figure shows that there are three sequers that are considered to be coinciding, that is, they are set using a similar equation.

By definition, it can be seen that the direct and its sequential in this case match up.

The sequential can crush the graph of the specified function plural. If there is an equation of the form y \u003d 0 for the unit, then the number of intersection points with sinusoid is infinite.

Definition 5.

Tangent to graphics function f (x) at point x 0; f (x 0) is called straight, passing through a specified point x 0; F (x 0), with the presence of a segment that has a plurality of x, close to x 0.

Example 1.

Consider in detail below the example above. Then it can be seen that the straight line, given by the function y \u003d x + 1, is considered tangent to Y \u003d 2 x at the point with coordinates (1; 2). For clarity, it is necessary to consider graphs with approximate to (1; 2) values. The function y \u003d 2 x is marked with black, the blue line is a tangent, the red point is the intersection point.

Obviously, y \u003d 2 x merges with a straight line y \u003d x + 1.

To determine the tangential one should consider the behavior of the tangent A B with an infinite approximation of the point in to point A. For clarity, we give the drawing.

The secant and B, designated with the help of a blue line, tends to the position of the tangent itself, and the angle of inclination α will strive to strive for the tilt angle of the tangent α x.

Definition 6.

Tangential to the graphics of the function y \u003d f (x) at the point A is considered the limit position of the sequential and in when in a tender to A, that is, B → a.

We now turn to the consideration of the geometric meaning of the derivative function at the point.

We turn to the consideration of the sequential A B for the function f (x), where A and B with coordinates x 0, f (x 0) and x 0 + δ x, f (x 0 + δ x), and Δ x we \u200b\u200bdenote as an argument increment . Now the function will take the form Δ y \u003d δ f (x) \u003d f (x 0 + δ x) - f (Δ x). For clarity, we give an example drawing.

Consider the obtained rectangular triangle A in C. We use the definition of tangent to solve, that is, we obtain the ratio Δ y Δ x \u003d T g α. From the determination of the tangent, it follows that Lim Δ X → 0 Δ Y Δ x \u003d T g α x. According to the rule of the derivative at the point, we have that the derivative F (x) at the point x 0 is called the limit of the relationship of the function to the increment of the argument, where Δ x → 0, then denote as f (x 0) \u003d Lim Δ x → 0 Δ y Δ x .

It follows that f "(x 0) \u003d Lim Δ x → 0 Δ y Δ x \u003d T g α x \u003d k x, where k x is denoted as an angular coefficient of tangential.

That is, we obtain that f '(x) can exist at point x 0 and as tangent to the specified graphics of the function at the touch point of x 0, F 0 (x 0), where the value of the angular coefficient of tangent at the point is derived at the point x 0. Then we get that k x \u003d f "(x 0).

The geometric meaning of the derivative function at the point is that the concept of existence of tangent to the schedule is given at the same point.

To record the equation of any direct on the plane, you must have an angular coefficient with a point through which it passes. Its designation is accepted as x 0 when crossing.

The equation tangent to the graph of the function y \u003d f (x) at point x 0, F 0 (x 0) takes the form y \u003d f "(x 0) · x - x 0 + f (x 0).

It is in mind that the final value of the derivative F "(x 0) can determine the position of the tangent, that is, vertically, under the condition Lim X → X 0 + 0 F" (x) \u003d ∞ and Lim X → X 0 - 0 F "(x ) \u003d ∞ or the absence at all, provided Lim X → X 0 + 0 F "(x) ≠ Lim X → x 0 - 0 F" (x).

The location of the tangent depends on the value of its angular coefficient KX \u003d F "(x 0). When parallelizing to the axis, we obtain that Kk \u003d 0, with parallelism to o - kx \u003d ∞, and the type of equation of tangent x \u003d x 0 increases KX\u003e 0, decreases at KX< 0 .

Example 2.

To compile the equation tangent to the graph of the function y \u003d e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 at the point with coordinates (1; 3) with the definition of an angle of inclination.

Decision

By condition, we have that the function is determined for all valid numbers. We obtain that the point with coordinates specified by condition (1; 3) is a touch point, then x 0 \u003d - 1, f (x 0) \u003d - 3.

It is necessary to find the derivative at the point with the value - 1. We get that

y "\u003d Ex + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" \u003d \u003d Ex + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" \u003d EX + 1 + x 2 - 6 - 3 3 y "(x 0) \u003d y" (- 1) \u003d E - 1 + 1 + - 1 2 - 6 - 3 3 \u003d 3 3

The value f '(x) at the touch point is an angular coefficient of tangent, which is equal to the tilt tangent.

Then k x \u003d t g α x \u003d y "(x 0) \u003d 3 3

It follows that α x \u003d a r c t g 3 3 \u003d π 6

Answer:the equation of tangent acquires the view

y \u003d f "(x 0) · x - x 0 + f (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3

For clarity, we give an example in graphic illustration.

Black color is used for original function graphic, blue color - image of tangent, red dot - touch point. The drawing, located on the right, shows in an enlarged form.

Example 3.

Find out the existence of a tangent to the schedule of a given function.
y \u003d 3 · x - 1 5 + 1 at point with coordinates (1; 1). Make the equation and determine the angle of inclination.

Decision

By condition, we have that the area of \u200b\u200bdefinition of a given function is considered to be the set of all valid numbers.

Let us turn to finding a derivative

y "\u003d 3 · x - 1 5 + 1" \u003d 3 · 1 5 · (x - 1) 1 5 - 1 \u003d 3 5 · 1 (x - 1) 4 5

If x 0 \u003d 1, then f '(x) is not defined, but the limits are recorded as Lim X → 1 + 0 3 5 · 1 (x - 1) 4 5 \u003d 3 5 · 1 (+ 0) 4 5 \u003d 3 5 · 1 + 0 \u003d + ∞ and Lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 \u003d 3 5 · 1 (- 0) 4 5 \u003d 3 5 · 1 + 0 \u003d + ∞, which means existence vertical tangent at point (1; 1).

Answer: The equation will take the form x \u003d 1, where the angle of inclination will be equal to π 2.

For clarity, depict graphically.

Example 4.

Find the point of schedule of the function y \u003d 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, where

1. Tangency does not exist;
2. Tangency is located in parallel about x;
3. Tanner parallel direct y \u003d 8 5 x + 4.

Decision

It is necessary to pay attention to the definition area. By condition, we have that the function is determined on the set of all valid numbers. Reveal the module and solve the system with gaps x ∈ - ∞; 2 and [- 2; + ∞). We get that

y \u003d - 1 15 x 3 + 18 x 2 + 105 x + 176, x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12, x ∈ [- 2; + ∞)

It is necessary to directly delete the function. We have that

y "\u003d - 1 15 x 3 + 18 x 2 + 105 x + 176", x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [- 2; + ∞) ⇔ y" \u003d - 1 5 (x 2 + 12 x + 35), x ∈ - ∞; - 2 1 5 x 2 - 4 x + 3, x ∈ [- 2; + ∞)

When x \u003d - 2, then the derivative does not exist, because one-sided limits are not equal at this point:

lim X → - 2 - 0 Y "(x) \u003d Lim X → - 2 - 0 - 1 5 (x 2 + 12 x + 35 \u003d - 1 5 (- 2) 2 + 12 (- 2) + 35 \u003d - 3 Lim X → - 2 + 0 y "(x) \u003d Lim X → - 2 + 0 1 5 (x 2 - 4 x + 3) \u003d 1 5 - 2 2 - 4 - 2 + 3 \u003d 3

Calculate the value of the function at the point x \u003d - 2, where we get that

1. y (- 2) \u003d 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 \u003d - 2, that is, tangent at point (- 2; - 2) will not exist.
2. Tanner parallel about X, when an angular coefficient is zero. Then KX \u003d TG α x \u003d f "(x 0). That is, it is necessary to find the values \u200b\u200bof such x, when the derivative of the function turns it into zero. That is, the values \u200b\u200bf '(x) and will be a touch point where the tangent is parallel to x .

When x ∈ - ∞; - 2, then - 1 5 (x 2 + 12 x + 35) \u003d 0, and at x ∈ (- 2; + ∞) we obtain 1 5 (x 2 - 4 x + 3) \u003d 0.

1 5 (x 2 + 12 x + 35) \u003d 0 d \u003d 12 2 - 4 · 35 \u003d 144 - 140 \u003d 4 x 1 \u003d - 12 + 4 2 \u003d - 5 ∈ - ∞; - 2 x 2 \u003d - 12 - 4 2 \u003d - 7 ∈ - ∞; - 2 1 5 (x 2 - 4 x + 3) \u003d 0 d \u003d 4 2 - 4 · 3 \u003d 4 x 3 \u003d 4 - 4 2 \u003d 1 ∈ - 2; + ∞ x 4 \u003d 4 + 4 2 \u003d 3 ∈ - 2; + ∞.

Calculate the corresponding values \u200b\u200bof the function

y 1 \u003d y - 5 \u003d 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 \u003d 8 5 y 2 \u003d y (- 7) \u003d 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 \u003d 4 3 y 3 \u003d y (1) \u003d 1 15 1 + 2 3 - 4 5 · 1 2 - 16 5 · 1 - 26 5 + 3 1 + 2 \u003d 8 5 y 4 \u003d y (3) \u003d 1 15 3 + 2 3 - 4 5 · 3 2 - 16 5 · 3 - 26 5 + 3 3 + 2 \u003d 4 3

Hence - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 are considered to be the desired points of the function graphics.

Consider a graphic image of the solution.

Black line - function graph, red dots - touch points.

1. When the straight lines are parallel, then the angular coefficients are equal. Then it is necessary to search for points of the graph of the function, where the corner coefficient will be equal to the value of 8 5. To do this, it is necessary to solve the equation of the form y "(x) \u003d 8 5. Then, if x ∈ - ∞; - 2, we obtain that - 1 5 (x 2 + 12 x + 35) \u003d 8 5, and if x ∈ ( - 2; + ∞), then 1 5 (x 2 - 4 x + 3) \u003d 8 5.

The first equation does not have roots, since the discriminant is less than zero. We write out what

1 5 x 2 + 12 x + 35 \u003d 8 5 x 2 + 12 x + 43 \u003d 0 d \u003d 12 2 - 4 · 43 \u003d - 28< 0

Another equation has two valid roots, then

1 5 (x 2 - 4 x + 3) \u003d 8 5 x 2 - 4 x - 5 \u003d 0 d \u003d 4 2 - 4 · (- 5) \u003d 36 x 1 \u003d 4 - 36 2 \u003d - 1 ∈ - 2; + ∞ x 2 \u003d 4 + 36 2 \u003d 5 ∈ - 2; + ∞.

Let us turn to finding the values \u200b\u200bof the function. We get that

y 1 \u003d y (- 1) \u003d 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 \u003d 4 15 y 2 \u003d y (5) \u003d 1 15 5 + 2 3 - 4 5 · 5 2 - 16 5 · 5 - 26 5 + 3 5 + 2 \u003d 8 3

Points with values \u200b\u200b- 1; 4 15, 5; 8 3 are points in which tangent parallel straight y \u003d 8 5 x + 4.

Answer:black Line - Function graph, Red line - graph Y \u003d 8 5 x + 4, Blue line - tangents at points - 1; 4 15, 5; 8 3.

The existence of an infinite number of tangents for specified functions is possible.

Example 5.

Write equations of all available tangential functions y \u003d 3 cos 3 2 x - π 4 - 1 3, which are perpendicular to the straight line y \u003d - 2 x + 1 2.

Decision

To compile the equation of the tangent, it is necessary to find the coefficient and coordinates of the point of touch, based on the condition of the perpendicularity of direct. The definition sounds like this: the product of the angular coefficients that are perpendicular to the direct, equal to 1, that is, written as k x · k ⊥ \u003d - 1. From the condition, we have that the angular coefficient is perpendicular to the line and equals k ⊥ \u003d - 2, then k x \u003d - 1 k ⊥ \u003d - 1 - 2 \u003d 1 2.

Now you need to find the coordinates of the point of touch. It is necessary to find x, after which its value is for a given function. Note that from the geometric meaning of the derivative at the point
x 0 We obtain that k x \u003d y "(x 0). From this equality, we will find the values \u200b\u200bof x for the touch points.

We get that

y "(x 0) \u003d 3 cos 3 2 x 0 - π 4 - 1 3" \u003d 3 · - sin 3 2 x 0 - π 4 · 3 2 x 0 - π 4 "\u003d \u003d - 3 · sin 3 2 x 0 - π 4 · 3 2 \u003d - 9 2 · sin 3 2 x 0 - π 4 ⇒ kx \u003d y "(x 0) ⇔ - 9 2 · sin 3 2 x 0 - π 4 \u003d 1 2 ⇒ SIN 3 2 x 0 - π 4 \u003d - 1 9

This trigonometric equation will be used to calculate the quantity of the touch points.

3 2 x 0 - π 4 \u003d a r c sin - 1 9 + 2 πk or 3 2 x 0 - π 4 \u003d π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 \u003d - a r c sin 1 9 + 2 πk or 3 2 x 0 - π 4 \u003d π + a r c sin 1 9 + 2 πk

x 0 \u003d 2 3 π 4 - a r c sin 1 9 + 2 πk or x 0 \u003d 2 3 5 π 4 + a r c sin 1 9 + 2 πk, k ∈ Z

Z - Many integers.

Found x Points of touch. Now you need to go to search for values \u200b\u200bfrom:

y 0 \u003d 3 cos 3 2 x 0 - π 4 - 1 3

y 0 \u003d 3 · 1 - sin 2 3 2 x 0 - π 4 - 1 3 or y 0 \u003d 3 · - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 \u003d 3 · 1 - - 1 9 2 - 1 3 or y 0 \u003d 3 · - 1 - - 1 9 2 - 1 3

y 0 \u003d 4 5 - 1 3 or y 0 \u003d - 4 5 + 1 3

From here we obtain that 2 3 π 4 - a r c sin 1 9 + 2 πk; 4 5 - 1 3, 2 3 5 π 4 + A R c sin 1 9 + 2 πk; - 4 5 + 1 3 are touch points.

Answer: needed equations will be recorded as

y \u003d 1 2 x - 2 3 π 4 - arc sin 1 9 + 2 πk + 4 5 - 1 3, y \u003d 1 2 x - 2 3 5 π 4 + arc sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

For a visual image, we consider the function and tangent on the coordinate direct.

The drawing shows that the location of the function goes on the interval [- 10; 10], where black strap is a function graph, blue lines - tangents, which are located perpendicular to a given direct form Y \u003d 2 x + 1 2. Red dots are touch points.

Canonical equations of curves 2 orders are not unambiguous features. The equations of tangents for them are compiled by known schemes.

Tangent of circle

To specify the circle with the center at the point x C E N T E R; Y C E N T E R and R radius is used by the formula X - X C E N T E R 2 + Y - Y C E N T E R 2 \u003d R 2.

This equality can be recorded as a combination of two functions:

y \u003d R 2 - X - X C E N T E R 2 + Y C E N T E R Y \u003d - R 2 - X - X C E N T E R 2 + Y C E N T E R

The first function is located at the top, and the second below, as shown in the figure.

To compile the circle equation at point x 0; Y 0, which is located in the upper or lower semicircle, it should be found equation of a graph of the function of the form y \u003d R 2 - x - x C E N T E R 2 + Y C E N T E R or Y \u003d - R 2 - X - X C E N T E R 2 + Y C E N T E R at the specified point.

When at the points x C E n T E R; y C E N T E R + R and X C E N T E R; y C E N T E R - R tangents can be set by the equations y \u003d y C E N T E R + R and Y \u003d y C E N T E R - R, and at points x C E N T E R + R; y c e n t e r and
X C E N T E R - R; Y C E N T E R will be parallel about y, then we obtain the equation of the form x \u003d x C E n T E R + R and X \u003d x C E N T E R - R.

Tangent to ellipse

When the ellipse has a center at point x C E N T E R; Y C E N T E R with semi-axles A and B, then it can be set using the X - X C E N T E R 2 A 2 + Y - Y - Y C E N T E R 2 B 2 \u003d 1.

Ellipse and circle can be denoted by combining two functions, namely: upper and lower half-elix. Then we get that

y \u003d b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y \u003d - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

If the tangents are located on the vertices of the ellipse, then they are parallel to X or O. Below for clarity, consider the drawing.

Example 6.

Write the equation tangent to the ellipse X - 3 2 4 + y - 5 2 25 \u003d 1 at points with the values \u200b\u200bof x equal to x \u003d 2.

Decision

It is necessary to find the touch points that correspond to the value x \u003d 2. We produce a substitution to the existing Ellipse equation and get that

x - 3 2 4 x \u003d 2 + y - 5 2 25 \u003d 1 1 4 + y - 5 2 25 \u003d 1 ⇒ y - 5 2 \u003d 3 4 · 25 ⇒ y \u003d ± 5 3 2 + 5

Then 2; 5 3 2 + 5 and 2; - 5 3 2 + 5 are touchpoints that belong to the upper and lower semi-ellipse.

Let us turn to finding and resolving the ellipse equation regarding Y. We get that

x - 3 2 4 + y - 5 2 25 \u003d 1 y - 5 2 25 \u003d 1 - x - 3 2 4 (y - 5) 2 \u003d 25 · 1 - x - 3 2 4 y - 5 \u003d ± 5 · 1 - x - 3 2 4 y \u003d 5 ± 5 2 4 - x - 3 2

It is obvious that the upper half-elix is \u200b\u200bset using the function of the form y \u003d 5 + 5 2 4 - x - 3 2, and the lower y \u003d 5 - 5 2 4 - x - 3 2.

Apply a standard algorithm in order to draw up the equation tangent to the graphics of the function at the point. We write that the equation is for the first tangent at point 2; 5 3 2 + 5 will be viewed

y "\u003d 5 + 5 2 4 - x - 3 2" \u003d 5 2 · 1 2 4 - (x - 3) 2 · 4 - (x - 3) 2 "\u003d \u003d - 5 2 · x - 3 4 - ( x - 3) 2 ⇒ y "(x 0) \u003d y" (2) \u003d - 5 2 · 2 - 3 4 - (2 - 3) 2 \u003d 5 2 3 ⇒ y \u003d y "(x 0) · x - x 0 + y 0 ⇔ y \u003d 5 2 3 (x - 2) + 5 3 2 + 5

We obtain that the equation of the second tangent with the value at the point
2; - 5 3 2 + 5 takes

y "\u003d 5 - 5 2 4 - (x - 3) 2" \u003d - 5 2 · 1 2 4 - (x - 3) 2 · 4 - (x - 3) 2 "\u003d \u003d 5 2 · x - 3 4 - (x - 3) 2 ⇒ y "(x 0) \u003d y" (2) \u003d 5 2 · 2 - 3 4 - (2 - 3) 2 \u003d - 5 2 3 ⇒ y \u003d y "(x 0) · x - x 0 + y 0 ⇔ y \u003d - 5 2 3 (x - 2) - 5 3 2 + 5

Graphically tangents are referred to as:

Tangent to hyperbole

When the hyperbole has a center at point x C E N T E R; y C E N T E R and the vertices x C E n T E R + α; y C E N T E R and X C E N T E R - α; y C E N T E R, there is a setting of inequality X - X C E N T E R 2 α 2 - y - Y C E N T E R 2 B 2 \u003d 1, if with the vertices x C e n t e r; y C E N T E R + B and X C E N T E R; Y C E N T E R - B, then it is set using an inequality X - X C E N T E R 2 α 2 - y - y C E N T E R 2 B 2 \u003d - 1.

The hyperbole can be represented as two combined functions of the form.

y \u003d Ba · (x - xCenter) 2 - a 2 + yCenterY \u003d - Ba · (x - xCenter) 2 - a 2 + yCenter or Y \u003d Ba · (x - xCenter) 2 + A 2 + YCENTERY \u003d - BA (X - XCenter) 2 + A 2 + YCENTER

In the first case, we have that tangents are parallel to y, and in the second parallel to x.

It follows that in order to find the equation of tangent of hyperbola, it is necessary to find out which function belongs to the touch point. To determine this, it is necessary to make a substitution in the equation and check them for identity.

Example 7.

Make an equation tangent to hyperbole x - 3 2 4 - y + 3 2 9 \u003d 1 at point 7; - 3 3 - 3.

Decision

It is necessary to transform the recording of the solution to find hyperboles using 2 functions. We get that

x - 3 2 4 - y + 3 2 9 \u003d 1 ⇒ y + 3 2 9 \u003d x - 3 2 4 - 1 ⇒ y + 3 2 \u003d 9 · x - 3 2 4 - 1 ⇒ y + 3 \u003d 3 2 · x - 3 2 - 4 and l and y + 3 \u003d - 3 2 · x - 3 2 - 4 ⇒ y \u003d 3 2 · x - 3 2 - 4 - 3 y \u003d - 3 2 · x - 3 2 - 4 - 3.

It is necessary to identify what function is the specified point with coordinates 7; - 3 3 - 3.

Obviously, to test the first function, it is necessary y (7) \u003d 3 2 · (7 - 3) 2 - 4 - 3 \u003d 3 3 - 3 ≠ - 3 3 - 3, then the point does not belong to the graph, since the equality is not performed.

For the second function, we have that y (7) \u003d - 3 2 · (7 - 3) 2 - 4 - 3 \u003d 3 3 - 3 ≠ - 3 3 - 3, it means that the point belongs to the specified graph. From here you should find an angular coefficient.

We get that

y "\u003d - 3 2 · (x - 3) 2 - 4 - 3" \u003d - 3 2 · x - 3 (x - 3) 2 - 4 ⇒ kx \u003d y "(x 0) \u003d - 3 2 · x 0 - 3 x 0 - 3 2 - 4 x 0 \u003d 7 \u003d - 3 2 · 7 - 3 7 - 3 2 - 4 \u003d - 3

Answer: The equation of tangent can be represented as

y \u003d - 3 · x - 7 - 3 3 - 3 \u003d - 3 · x + 4 3 - 3

Clearly depicted like this:

Tangent to parabole

To make an equation tangent to parabole Y \u003d AX 2 + BX + C at point x 0, y (x 0), it is necessary to use a standard algorithm, then the equation will take the form y \u003d y "(x 0) · x - x 0 + y ( x 0). Such a tangent in the top parallel to x.

You should specify parabola x \u003d a y 2 + b y + c as a combination of two functions. Therefore, it is necessary to resolve the equation relative to y. We get that

x \u003d AY 2 + BY + C ⇔ AY 2 + BY + C - X \u003d 0 D \u003d B 2 - 4 A (C - X) Y \u003d - B + B 2 - 4 A (C - X) 2 AY \u003d - B - B 2 - 4 A (C - X) 2 A

Graphically shown like:

To clarify the accessories of the point x 0, y (x 0) functions, gently act according to the standard algorithm. Such a tangent will be parallel to the relatively parabola.

Example 8.

Write an equation tangent to graph x - 2 y 2 - 5 y + 3, when we have an angle of inclination of 150 °.

Decision

We begin a solution from the view of the parabola as two functions. We get that

2 y 2 - 5 y + 3 - x \u003d 0 d \u003d (- 5) 2 - 4 · (- 2) · (3 - x) \u003d 49 - 8 xy \u003d 5 + 49 - 8 x - 4 y \u003d 5 - 49 - 8 x - 4

The value of the angular coefficient is equal to the value of the derivative at the point x 0 of this function and is equal to the tangent of the angle of inclination.

We get:

k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3

From here we define the value of x for the point of touch.

The first function will be recorded as

y "\u003d 5 + 49 - 8 x - 4" \u003d 1 49 - 8 x ⇒ y "(x 0) \u003d 1 49 - 8 x 0 \u003d - 1 3 ⇔ 49 - 8 x 0 \u003d - 3

Obviously, there are no valid roots, since they got a negative value. We conclude that there is no tangent with an angle of 150 ° for such a function.

The second function will be recorded as

y "\u003d 5 - 49 - 8 x - 4" \u003d - 1 49 - 8 x ⇒ y "(x 0) \u003d - 1 49 - 8 x 0 \u003d - 1 3 ⇔ 49 - 8 x 0 \u003d - 3 x 0 \u003d 23 4 ⇒ Y (x 0) \u003d 5 - 49 - 8 · 23 4 - 4 \u003d - 5 + 3 4

We have that touchpoints are 23 4; - 5 + 3 4.

Answer: The tangent equation takes the form

y \u003d - 1 3 · X - 23 4 + - 5 + 3 4

Graphically will shown it in this way:

If you notice a mistake in the text, please select it and press Ctrl + Enter

Example 1. Dana feature f.(x.) = 3x. 2 + 4x. - 5. Write equation tangent to the graph f.(x.) At the point of schedule with the abscissa x. 0 = 1.

Decision. Derived function f.(x.) exists for any x R. . Find her:

= (3x. 2 + 4x. - 5) '\u003d 6 x. + 4.

Then f.(x. 0) = f.(1) = 2; (x. 0) \u003d \u003d 10. The equation of tangent has the form:

y. = (x. 0) (x. – x. 0) + f.(x. 0),

y. = 10(x. – 1) + 2,

y. = 10x. – 8.

Answer. y. = 10x. – 8.

Example 2. Dana feature f.(x.) = x. 3 – 3x. 2 + 2x. + 5. Write equation tangent to graphics function f.(x.), parallel direct Y. = 2x. – 11.

Decision. Derived function f.(x.) exists for any x R. . Find her:

= (x. 3 – 3x. 2 + 2x. + 5) '\u003d 3 x. 2 – 6x. + 2.

As tangent to graphics function f.(x.) at the point with the abscissa x. 0 parallel to direct Y. = 2x. - 11, then its angular coefficient is 2, i.e. ( x. 0) \u003d 2. We will find this abscissa from the condition that 3 x.– 6x. 0 + 2 \u003d 2. This equality is valid only when x. 0 \u003d 0 and when x. 0 \u003d 2. Since in that and in another case f.(x. 0) \u003d 5, then straight y. = 2x. + b. Regards the graph of the function or at point (0; 5), or at point (2; 5).

In the first case, the numeric equality is 5 \u003d 2 × 0 + b.From! b. \u003d 5, and in the second case, the numerical equality 5 \u003d 2 × 2 + b.From! b. = 1.

So there are two tangents y. = 2x. + 5 I. y. = 2x. + 1 to graphics function f.(x.), parallel direct Y. = 2x. – 11.

Answer. y. = 2x. + 5, y. = 2x. + 1.

Example 3. Dana feature f.(x.) = x. 2 – 6x. + 7. Write equation tangent to function graphics f.(x.) passing through the point A. (2; –5).

Decision. As f.(2) -5, then the point A. does not belong to the graphics function f.(x.). Let be x. 0 - abscissa point of touch.

Derived function f.(x.) exists for any x R. . Find her:

= (x. 2 – 6x. + 1) '\u003d 2 x. – 6.

Then f.(x. 0) = x.– 6x. 0 + 7; (x. 0) = 2x. 0 - 6. The tangent equation has the form:

y. = (2x. 0 – 6)(x. – x. 0) + x.– 6x.+ 7,

y. = (2x. 0 – 6)x.– x.+ 7.

Since point A. belongs to the tangent, then the numerical equality is true

–5 = (2x. 0 - 6) × 2- x.+ 7,

from x. 0 \u003d 0 or x. 0 \u003d 4. This means that through the point A.you can spend two tangents for graphics function f.(x.).

If a x. 0 \u003d 0, the tangent equation is y. = –6x. + 7. If x. 0 \u003d 4, the tangent equation has the form y. = 2x. – 9.

Answer. y. = –6x. + 7, y. = 2x. – 9.

Example 4. Functions are given f.(x.) = x. 2 – 2x. + 2 I. g.(x.) = –x. 2 - 3. Write the equation to the total tangent to the graphs of these functions.

Decision. Let be x. 1 - Absissance Points of Touch Skeeping Direct With Function Schedule f.(x.), but x. 2 - Absissance Points of Touch the same direct with a function schedule g.(x.).

Derived function f.(x.) exists for any x R. . Find her:

= (x. 2 – 2x. + 2) '\u003d 2 x. – 2.

Then f.(x. 1) = x.– 2x. 1 + 2; (x. 1) = 2 X. 1 - 2. The equation of the tangent has the form:

y. = (2x. 1 – 2)(x. – x. 1) + x.– 2x. 1 + 2,

Y. = (2x. 1 – 2)x. – x.+ 2. (1)

Find a derivative function g.(x.):

= (–x. 2 - 3) '\u003d -2 x..

Y \u003d F (x) and if at this point to the graph of the function can be tanged, not perpendicular to the abscissa axis, then the angular coefficient of tangent is f "(a). We have already used it several times. For example, in § 33 it was found that the graph of the function y \u003d sin x (sinusoid) at the beginning of the coordinate forms an angle of 45 ° with the abscissa axis (more precisely, the tangent to the graph at the beginning of the coordinate is with a positive direction of the axis x angle 45 °), and in Example 5 § 33 points on graphic set functionsin which the tangency is parallel to the abscissa axis. In Example 2 § 33, an equation tangent to the graphics of the function y \u003d x 2 at point x \u003d 1 (more precisely, at point (1; 1), but more often indicate the abscissa value, believing that if the abscissa value is known, the value of the ordinate It can be found from the equation y \u003d f (x)). In this paragraph, we will develop an algorithm for the preparation of the equation of tangent. For the schedule of any function.

Let the function y \u003d f (x) and point M (a; f (a)), and also it is known that there exists f "(a). To make an equation tangent to a graph of a given function at a given point. This equation as equation any The straight, non-parallel axis of the ordinate, has the form y \u003d kx + m, so the task is to find the values \u200b\u200bof coefficients to and m.

With an angular coefficient for problems there is no: we know that K \u003d F "(a). To calculate the value of T, we use the fact that the desired direct passes through the point M (A; F (a)). This means that if you substitute the coordinates Points m to the equation are direct, we obtain the right equality: f (a) \u003d ka + m, from where we find that m \u003d f (a) - ka.
It remains to substitute the found values \u200b\u200bof the whale coefficients in the equation straight:

We obtained the equation tangent to the graph of the function y \u003d f (x) at the point x \u003d a.
If, say,
Substituting in equation (1) the found values \u200b\u200bof a \u003d 1, f (a) \u003d 1 f "(a) \u003d 2, we obtain: y \u003d 1 + 2 (x - f), i.e. y \u003d 2x-1.
Compare this result with what was obtained in Example 2 from § 33. Naturally, it turned out the same.
We will make equation tangent to graphics of the function y \u003d TG x at the beginning of the coordinates. We have: So, COs X F "(0) \u003d 1. Substitting into equation (1) the values \u200b\u200bfound a \u003d 0, f (a) \u003d 0, f" (a) \u003d 1, we obtain: y \u003d x.
That is why we conducted a tangentsoid in § 15 (see Fig. 62) through the origin at the angle of 45 ° to the abscissa axis.
Solving these fairly simple examples, we actually used a certain algorithm, which is laid in formula (1). We will make this algorithm explicit.

Algorithm forcing the equation of tangential to graphics function y \u003d f (x)

1) Label the abscissa of the touch point of the letter a.
2) Calculate 1 (a).
3) Find F "(x) and calculate F" (a).
4) substitute the found numbers a, f (a), (a) in formula (1).

Example 1. Make the equation tangent to the graph of the function at point x \u003d 1.
We use the algorithm, given that in this example

In fig. 126 depicts hyperbole, built straight y \u003d 2.
The drawing confirms the above calculations: Indeed, straight y \u003d 2 to the hyperboles at the point (1; 1).

Answer: y \u003d 2nd.
Example 2.To the graphics of the function to conduct a tangent so that it be parallel to the straight y \u003d 4x - 5.
We clarify the wording of the problem. The requirement to "conduct a tangent" usually means "draw up the equation of tangent." It is logical, for if a person was able to make an equation of tangent, it is unlikely that it will hardly experience difficulties in the coordinate plane of direct equation.
We use the algorithm for the compilation of the equation of the tangent, given that in this example, but in contrast to the previous example there is an ambiguity: not specified is clearly the abscissa point of touch.
Let's start talking like this. The desired tangent must be parallel to the direct y \u003d 4x-5. Two straight parallels then and only if their angular coefficients are equal. So, the angular coefficient of tangent must be equal to the angular coefficient of the specified direct: Thus, the value and we can find from the equation F "(a) \u003d 4.
We have:
It means from the equation, there are two tangents that satisfy the condition of the problem: one at a point with abscissa 2, the other at the point with the abscissa -2.
Now you can act on the algorithm.

Example 3. From the point (0; 1) to conduct a tangent to the graph
We use the algorithm to compile the equation of tangent, given that in this example, we note that here, as in Example 2, the touch point is clearly not specified. Nevertheless, we act on the algorithm.

By condition, the tangent passes through the point (0; 1). Substituting in equation (2) the values \u200b\u200bx \u003d 0, y \u003d 1, we get:
As you can see, in this example, only at the fourth step of the algorithm we managed to find the abscissa point of touch. Substituting the value A \u003d 4 in equation (2), we get:

In fig. 127 presents a geometric illustration of the considered example: a function schedule

In § 32, we noted that for the function y \u003d f (x), which has a derivative in a fixed point x, is fairly approximate equality:

For the convenience of further reasoning, we will change the designation: instead of how we will write a, instead we will write x and, accordingly, instead we will write xh. Then the above-mentioned equality will take the form:

And now take a look in fig. 128. The function of the function y \u003d f (x) was tested at the point M (A; F (a)). The point x is noted on the abscissa axis close from a. It is clear that f (x) - the ordinate graph of the function at the specified point x. And what is F (a) + f "(a) (x - a)? This is the ordinate of the tangent, corresponding to the same point x - see formula (1). What is the meaning of approximate equality (3)? Is that To calculate the approximate value of the function take the value of the ordinate tangent.

Example 4. Find the approximate value of the numerical expression 1.02 7.
It is about finding the value of the function y \u003d x 7 at the point x \u003d 1.02. We use the formula (3), taking into account that in this example
As a result, we get:

If we use the calculator, we will get: 1.02 7 \u003d 1,148685667 ...
As you can see, the accuracy of the approximation is quite acceptable.
Answer: 1,02 7 =1,14.

A.G. Mordkovich Algebra Grade 10

Calendar and thematic planning in mathematics, video in mathematics online, mathematics at school download

Design of lesson Abstract lesson reference frame presentation lesson accelerative methods interactive technologies Practice Tasks and exercises self-test Workshop, trainings, cases, quests Home tasks Discussion issues Rhetorical questions from students Illustrations Audio, video clips and multimedia Photos, pictures, tables, Schemes of humor, jokes, jokes, Comics Proverbs, sayings, crosswords, quotes Supplements Abstracts Articles Chips for Curious Cheat Sheets Textbooks Basic and Additional Globes Other Terms Improving textbooks and lessons Fixing errors in the textbook Updating fragment in the textbook. Innovation elements in the lesson replacing outdated knowledge new Only for teachers Perfect lessons Calendar Plan for the year Methodical recommendations of the discussion program Integrated lessons