Quadratic equations d 0. Quadratic equation

Landscape design and planning

Kopyevskaya rural secondary school

10 Ways to Solve Quadratic Equations

Head: Patrikeeva Galina Anatolyevna,

mathematic teacher

1. History of the development of quadratic equations

1.1 Quadratic equations in Ancient Babylon

1.2 How Diophantus compiled and solved quadratic equations

1.3 Quadratic equations in India

1.4 Quadratic equations by al-Khorezmi

1.5 Quadratic equations in Europe XIII - XVII centuries

1.6 About Vieta's theorem

2. Methods for solving quadratic equations

Conclusion

Literature

1. History of the development of quadratic equations

1.1 Quadratic equations in Ancient Babylon

The need to solve equations not only of the first, but also of the second degree in ancient times was caused by the need to solve problems related to finding areas land plots and with earthworks of a military nature, as well as with the development of astronomy and mathematics itself. Quadratic equations could be solved around 2000 BC. e. Babylonians.

Using modern algebraic notation, we can say that in their cuneiform texts there are, in addition to incomplete ones, such, for example, complete quadratic equations:

X 2 + X = ¾; X 2 - X = 14,5

The rule for solving these equations, set out in the Babylonian texts, essentially coincides with the modern one, but it is not known how the Babylonians arrived at this rule. Almost all cuneiform texts found so far provide only problems with solutions laid out in the form of recipes, with no indication as to how they were found.

Despite high level development of algebra in Babylon, the cuneiform texts lack the concept of a negative number and general methods for solving quadratic equations.

1.2 How Diophantus composed and solved quadratic equations.

Diophantus' Arithmetic does not contain a systematic presentation of algebra, but it contains a systematic series of problems, accompanied by explanations and solved by constructing equations of various degrees.

When composing equations, Diophantus skillfully selects unknowns to simplify the solution.

Here, for example, is one of his tasks.

Problem 11.“Find two numbers, knowing that their sum is 20 and their product is 96”

Diophantus reasons as follows: from the conditions of the problem it follows that the required numbers are not equal, since if they were equal, then their product would not be equal to 96, but to 100. Thus, one of them will be more than half of their sum, i.e. . 10 + x, the other is less, i.e. 10's. The difference between them 2x .

Hence the equation:

(10 + x)(10 - x) = 96

100 - x 2 = 96

x 2 - 4 = 0 (1)

From here x = 2. One of the required numbers is equal to 12 , other 8 . Solution x = -2 for Diophantus does not exist, since Greek mathematics knew only positive numbers.

If we solve this problem by choosing one of the required numbers as the unknown, then we will come to a solution to the equation

y(20 - y) = 96,

y 2 - 20y + 96 = 0. (2)

It is clear that by choosing the half-difference of the required numbers as the unknown, Diophantus simplifies the solution; he manages to reduce the problem to solving an incomplete quadratic equation (1).

1.3 Quadratic Equations in India

Problems on quadratic equations are found already in the astronomical treatise “Aryabhattiam”, compiled in 499 by the Indian mathematician and astronomer Aryabhatta. Another Indian scientist, Brahmagupta (7th century), outlined general rule solutions of quadratic equations reduced to a single canonical form:

ah 2 + b x = c, a > 0. (1)

In equation (1), the coefficients, except A, can also be negative. Brahmagupta's rule is essentially the same as ours.

IN Ancient India Public competitions in solving difficult problems were common. One of the old Indian books says the following about such competitions: “As the sun outshines the stars with its brilliance, so a learned man will outshine the glory of another in public assemblies, proposing and solving algebraic problems.” Problems were often presented in poetic form.

This is one of the problems of the famous Indian mathematician of the 12th century. Bhaskars.

Problem 13.

“A flock of frisky monkeys, and twelve along the vines...

The authorities, having eaten, had fun. They started jumping, hanging...

There are them in the square, part eight. How many monkeys were there?

I was having fun in the clearing. Tell me, in this pack?

Bhaskara's solution indicates that he knew that the roots of quadratic equations are two-valued (Fig. 3).

The equation corresponding to problem 13 is:

( x /8) 2 + 12 = x

Bhaskara writes under the guise:

x 2 - 64x = -768

and, to complete the left side of this equation to square, adds to both sides 32 2 , then getting:

x 2 - 64x + 32 2 = -768 + 1024,

(x - 32) 2 = 256,

x - 32 = ± 16,

x 1 = 16, x 2 = 48.

1.4 Quadratic equations in al - Khorezmi

In the algebraic treatise of al-Khorezmi, a classification of linear and quadratic equations is given. The author counts 6 types of equations, expressing them as follows:

1) “Squares are equal to roots,” i.e. ax 2 + c = b X.

2) “Squares are equal to numbers”, i.e. ax 2 = c.

3) “The roots are equal to the number,” i.e. ah = s.

4) “Squares and numbers are equal to roots,” i.e. ax 2 + c = b X.

5) “Squares and roots are equal to numbers”, i.e. ah 2 + bx = s.

6) “Roots and numbers are equal to squares,” i.e. bx + c = ax 2 .

For al-Khorezmi, who avoided the use of negative numbers, the terms of each of these equations are addends and not subtractables. In this case, equations that do not have positive solutions are obviously not taken into account. The author sets out methods for solving these equations using the techniques of al-jabr and al-muqabala. His decisions, of course, do not completely coincide with ours. Not to mention that it is purely rhetorical, it should be noted, for example, that when solving an incomplete quadratic equation of the first type

al-Khorezmi, like all mathematicians before the 17th century, does not take into account the zero solution, probably because in specific practical problems it does not matter. When solving complete quadratic equations, al-Khorezmi sets out the rules for solving them using particular numerical examples, and then geometric proofs.

Problem 14.“The square and the number 21 are equal to 10 roots. Find the root" (implying the root of the equation x 2 + 21 = 10x).

The author's solution goes something like this: divide the number of roots in half, you get 5, multiply 5 by itself, subtract 21 from the product, what remains is 4. Take the root from 4, you get 2. Subtract 2 from 5, you get 3, this will be the desired root. Or add 2 to 5, which gives 7, this is also a root.

The treatise of al-Khorezmi is the first book that has come down to us, which systematically sets out the classification of quadratic equations and gives formulas for their solution.

1.5 Quadratic equations in Europe XIII - XVII bb

Formulas for solving quadratic equations along the lines of al-Khwarizmi in Europe were first set forth in the Book of Abacus, written in 1202 by the Italian mathematician Leonardo Fibonacci. This voluminous work, which reflects the influence of mathematics, both Islamic countries and Ancient Greece, is distinguished by both completeness and clarity of presentation. The author independently developed some new algebraic examples solving problems and was the first in Europe to introduce negative numbers. His book contributed to the spread of algebraic knowledge not only in Italy, but also in Germany, France and other European countries. Many problems from the Book of Abacus were used in almost all European textbooks of the 16th - 17th centuries. and partly XVIII.

The general rule for solving quadratic equations reduced to a single canonical form:

x 2 + bx = c,

for all possible combinations of coefficient signs b , With was formulated in Europe only in 1544 by M. Stiefel.

Derivation of the formula for solving a quadratic equation in general view Viet has it, but Viet recognized only positive roots. Italian mathematicians Tartaglia, Cardano, Bombelli were among the first in the 16th century. In addition to positive ones, negative roots are also taken into account. Only in the 17th century. Thanks to the work of Girard, Descartes, Newton and other scientists, the method of solving quadratic equations takes on a modern form.

1.6 About Vieta's theorem

The theorem expressing the relationship between the coefficients of a quadratic equation and its roots, named after Vieta, was formulated by him for the first time in 1591 as follows: “If B + D, multiplied by A - A 2 , equals BD, That A equals IN and equal D ».

To understand Vieta, we should remember that A, like any vowel letter, meant the unknown (our X), vowels IN, D- coefficients for the unknown. In the language of modern algebra, the above Vieta formulation means: if there is

(a + b )x - x 2 = ab ,

x 2 - (a + b )x + a b = 0,

x 1 = a, x 2 = b .

Expressing the relationship between the roots and coefficients of the equations general formulas written using symbols, Viet established uniformity in the methods of solving equations. However, the symbolism of Viet is still far from modern look. He did not recognize negative numbers and therefore, when solving equations, he considered only cases where all the roots were positive.

2. Methods for solving quadratic equations

Quadratic equations are the foundation on which the majestic edifice of algebra rests. Quadratic equations are found wide application when solving trigonometric, exponential, logarithmic, irrational and transcendental equations and inequalities. We all know how to solve quadratic equations from school (8th grade) until graduation.

Formulas for the roots of a quadratic equation. The cases of real, multiple and complex roots. Factoring a quadratic trinomial. Geometric interpretation. Examples of determining roots and factoring.

Basic formulas

Consider the quadratic equation:
(1) .
Roots of a quadratic equation(1) are determined by the formulas:
; .
These formulas can be combined like this:
.
When the roots of a quadratic equation are known, then a polynomial of the second degree can be represented as a product of factors (factored):
.

Next we assume that are real numbers.
Let's consider discriminant of a quadratic equation:
.
If the discriminant is positive, then the quadratic equation (1) has two different real roots:
; .
Then the factorization of the quadratic trinomial has the form:
.
If the discriminant is equal to zero, then the quadratic equation (1) has two multiple (equal) real roots:
.
Factorization:
.
If the discriminant is negative, then the quadratic equation (1) has two complex conjugate roots:
;
.
Here is the imaginary unit, ;
and are the real and imaginary parts of the roots:
; .
Then

.

Graphic interpretation

If you build graph of a function
,
which is a parabola, then the points of intersection of the graph with the axis will be the roots of the equation
.
At , the graph intersects the x-axis (axis) at two points.
When , the graph touches the x-axis at one point.
When , the graph does not cross the x-axis.

Below are examples of such graphs.

Useful formulas related to quadratic equation

(f.1) ;
(f.2) ;
(f.3) .

Derivation of the formula for the roots of a quadratic equation

We carry out transformations and apply formulas (f.1) and (f.3):




,
Where
; .

So, we got the formula for a polynomial of the second degree in the form:
.
This shows that the equation

performed at
And .
That is, and are the roots of the quadratic equation
.

Examples of determining the roots of a quadratic equation

Example 1

(1.1) .

Solution

.
Comparing with our equation (1.1), we find the values ​​of the coefficients:
.
We find the discriminant:
.
Since the discriminant is positive, the equation has two real roots:
;
;
.

From here we obtain the factorization of the quadratic trinomial:

.

Graph of the function y = 2 x 2 + 7 x + 3 intersects the x-axis at two points.

Let's plot the function
.
The graph of this function is a parabola. It crosses the abscissa axis (axis) at two points:
And .
These points are the roots of the original equation (1.1).

Answer

;
;
.

Example 2

Find the roots of a quadratic equation:
(2.1) .

Solution

Let's write the quadratic equation in general form:
.
Comparing with the original equation (2.1), we find the values ​​of the coefficients:
.
We find the discriminant:
.
Since the discriminant is zero, the equation has two multiple (equal) roots:
;
.

Then the factorization of the trinomial has the form:
.

Graph of the function y = x 2 - 4 x + 4 touches the x-axis at one point.

Let's plot the function
.
The graph of this function is a parabola. It touches the x-axis (axis) at one point:
.
This point is the root of the original equation (2.1). Since this root is factored twice:
,
then such a root is usually called a multiple. That is, they believe that there are two equal roots:
.

Answer

;
.

Example 3

Find the roots of a quadratic equation:
(3.1) .

Solution

Let's write the quadratic equation in general form:
(1) .
Let's rewrite the original equation (3.1):
.
Comparing with (1), we find the values ​​of the coefficients:
.
We find the discriminant:
.
The discriminant is negative, .

Therefore there are no real roots.
;
;
.

You can find complex roots:


.

Then

Let's plot the function
.
The graph of this function is a parabola. It does not intersect the x-axis (axis). Therefore there are no real roots.

Answer

There are no real roots. Complex roots:
;
;
.

It is known that it is a particular version of the equality ax 2 + bx + c = o, where a, b and c are real coefficients for unknown x, and where a ≠ o, and b and c will be zeros - simultaneously or separately. For example, c = o, b ≠ o or vice versa. We almost remembered the definition of a quadratic equation.

The second degree trinomial is zero. Its first coefficient a ≠ o, b and c can take any values. The value of the variable x will then be when substitution turns it into a correct numerical equality. Let's focus on real roots, although the equations can also be solutions. It is customary to call an equation complete in which none of the coefficients is equal to o, a ≠ o, b ≠ o, c ≠ o.
Let's solve an example. 2x 2 -9x-5 = oh, we find
D = 81+40 = 121,
D is positive, which means there are roots, x 1 = (9+√121):4 = 5, and the second x 2 = (9-√121):4 = -o.5. Checking will help make sure they are correct.

Here step by step solution quadratic equation

Using the discriminant, you can solve any equation on the left side of which there is a known quadratic trinomial for a ≠ o. In our example. 2x 2 -9x-5 = 0 (ax 2 +in+c = o)

Let's look at what there are incomplete equations second degree

1. ax 2 +in = o. The free term, the coefficient c at x 0, is equal to zero here, in ≠ o.
   How to solve an incomplete quadratic equation of this type? Let's take x out of brackets. Let us remember when the product of two factors is equal to zero.
   x(ax+b) = o, this can be when x = o or when ax+b = o.
   Having solved the 2nd we have x = -в/а.
   As a result, we have roots x 1 = 0, according to calculations x 2 = -b/a.
2. Now the coefficient of x is equal to o, and c is not equal (≠) o.
   x 2 +c = o. Let's move from to right side equality, we get x 2 = -с. This equation only has real roots when -c is a positive number (c ‹ o),
   x 1 is then equal to √(-c), respectively, x 2 is -√(-c). Otherwise, the equation has no roots at all.
3. The last option: b = c = o, that is, ax 2 = o. Naturally, such a simple equation has one root, x = o.

Special cases

We looked at how to solve an incomplete quadratic equation, and now let’s take any types.

• In a complete quadratic equation, the second coefficient of x is an even number.
  Let k = o.5b. We have formulas for calculating the discriminant and roots.
  D/4 = k 2 - ac, the roots are calculated as x 1,2 = (-k±√(D/4))/a for D › o.
  x = -k/a at D = o.
  There are no roots for D ‹ o.
• There are given quadratic equations, when the coefficient of x squared is equal to 1, they are usually written x 2 + рх + q = o. All the above formulas apply to them, but the calculations are somewhat simpler.
  Example, x 2 -4x-9 = 0. Calculate D: 2 2 +9, D = 13.
  x 1 = 2+√13, x 2 = 2-√13.
• In addition, it is easy to apply to those given. It says that the sum of the roots of the equation is equal to -p, the second coefficient with a minus (meaning the opposite sign), and the product of these same roots will be equal to q, the free term. See how easy it would be to determine the roots of this equation verbally. For unreduced coefficients (for all coefficients not equal to zero), this theorem is applicable as follows: the sum x 1 + x 2 is equal to -b/a, the product x 1 · x 2 is equal to c/a.

The sum of the free term c and the first coefficient a is equal to the coefficient b. In this situation, the equation has at least one root (easy to prove), the first one is necessarily equal to -1, and the second -c/a, if it exists. You can check how to solve an incomplete quadratic equation yourself. As easy as pie. The coefficients may be in certain relationships with each other

• x 2 +x = o, 7x 2 -7 = o.
• The sum of all coefficients is equal to o.
  The roots of such an equation are 1 and c/a. Example, 2x 2 -15x+13 = o.
  x 1 = 1, x 2 = 13/2.

There are a number of other ways to solve various second-degree equations. Here, for example, is a method for extracting a complete square from a given polynomial. There are several graphical methods. When you often deal with such examples, you will learn to “click” them like seeds, because all the methods come to mind automatically.

Quadratic equation - easy to solve! *Hereinafter referred to as “KU”. Friends, it would seem that there could be nothing simpler in mathematics than solving such an equation. But something told me that many people have problems with him. I decided to see how many on-demand impressions Yandex gives out per month. Here's what happened, look:

What does it mean? This means that about 70,000 people per month are searching for this information, what does this have to do with summer, and what will happen during the school year - there will be twice as many requests. This is not surprising, because those guys and girls who graduated from school a long time ago and are preparing for the Unified State Exam are looking for this information, and schoolchildren also strive to refresh their memory.

Despite the fact that there are a lot of sites that tell you how to solve this equation, I decided to also contribute and publish the material. Firstly, I would like visitors to come to my site based on this request; secondly, in other articles, when the topic of “KU” comes up, I will provide a link to this article; thirdly, I’ll tell you a little more about his solution than is usually stated on other sites. Let's get started! The content of the article:

A quadratic equation is an equation of the form:

where coefficients a,band c are arbitrary numbers, with a≠0.

IN school course the material is given in the following form - the equations are conventionally divided into three classes:

1. They have two roots.

2. *Have only one root.

3. They have no roots. It is worth especially noting here that they do not have real roots

How are roots calculated? Just!

We calculate the discriminant. Underneath this “terrible” word lies a very simple formula:

The root formulas are as follows:

*You need to know these formulas by heart.

You can immediately write down and solve:

Example:

1. If D > 0, then the equation has two roots.

2. If D = 0, then the equation has one root.

3. If D< 0, то уравнение не имеет действительных корней.

Let's look at the equation:

In this regard, when the discriminant is equal to zero, the school course says that one root is obtained, here it is equal to nine. Everything is correct, it is so, but...

This idea is somewhat incorrect. In fact, there are two roots. Yes, yes, don’t be surprised, you get two equal roots, and to be mathematically precise, then the answer should write two roots:

x 1 = 3 x 2 = 3

But it is so - small retreat. At school you can write it down and say that there is one root.

Now the next example:

As we know, the root of a negative number cannot be taken, so the solutions in in this case No.

That's the whole decision process.

Quadratic function.

This shows what the solution looks like geometrically. This is extremely important to understand (in the future, in one of the articles we will analyze in detail the solution to the quadratic inequality).

This is a function of the form:

where x and y are variables

a, b, c – given numbers, with a ≠ 0

The graph is a parabola:

That is, it turns out that by solving a quadratic equation with “y” equal to zero, we find the points of intersection of the parabola with the x axis. There can be two of these points (the discriminant is positive), one (the discriminant is zero) and none (the discriminant is negative). Details about quadratic function You can view article by Inna Feldman.

Let's look at examples:

Example 1: Solve 2x 2 +8 x–192=0

a=2 b=8 c= –192

D=b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Answer: x 1 = 8 x 2 = –12

*It was possible to immediately divide the left and right sides of the equation by 2, that is, simplify it. Calculations will be easier.

Example 2: Decide x 2–22 x+121 = 0

a=1 b=–22 c=121

D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

We found that x 1 = 11 and x 2 = 11

It is permissible to write x = 11 in the answer.

Answer: x = 11

Example 3: Decide x 2 –8x+72 = 0

a=1 b= –8 c=72

D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224

The discriminant is negative, there is no solution in real numbers.

Answer: no solution

The discriminant is negative. There is a solution!

Here we will talk about solving the equation in the case when a negative discriminant is obtained. Do you know anything about complex numbers? I will not go into detail here about why and where they arose and what their specific role and necessity in mathematics is; this is a topic for a large separate article.

The concept of a complex number.

A little theory.

A complex number z is a number of the form

z = a + bi

where a and b are real numbers, i is the so-called imaginary unit.

a+bi – this is a SINGLE NUMBER, not an addition.

The imaginary unit is equal to the root of minus one:

Now consider the equation:

We get two conjugate roots.

Incomplete quadratic equation.

Let's consider special cases, this is when the coefficient “b” or “c” is equal to zero (or both are equal to zero). They can be solved easily without any discriminatory issues.

Case 1. Coefficient b = 0.

The equation becomes:

Let's transform:

Example:

4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2

Case 2. Coefficient c = 0.

The equation becomes:

Let's transform and factorize:

*The product is equal to zero when at least one of the factors is equal to zero.

Example:

9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 or x–5 =0

x 1 = 0 x 2 = 5

Case 3. Coefficients b = 0 and c = 0.

Here it is clear that the solution to the equation will always be x = 0.

Useful properties and patterns of coefficients.

There are properties that allow you to solve equations with large coefficients.

Ax 2 + bx+ c=0 equality holds

a + b+ c = 0, That

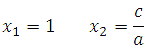
- if for the coefficients of the equation Ax 2 + bx+ c=0 equality holds

a+ s =b, That

These properties help solve a certain type of equation.

Example 1: 5001 x 2 –4995 x – 6=0

The sum of the odds is 5001+( – 4995)+(– 6) = 0, which means

Example 2: 2501 x 2 +2507 x+6=0

Equality holds a+ s =b, Means

Regularities of coefficients.

1. If in the equation ax 2 + bx + c = 0 the coefficient “b” is equal to (a 2 +1), and the coefficient “c” is numerically equal to the coefficient “a”, then its roots are equal

ax 2 + (a 2 +1)∙x+ a= 0 = > x 1 = –a x 2 = –1/a.

Example. Consider the equation 6x 2 + 37x + 6 = 0.

x 1 = –6 x 2 = –1/6.

2. If in the equation ax 2 – bx + c = 0 the coefficient “b” is equal to (a 2 +1), and the coefficient “c” is numerically equal to the coefficient “a”, then its roots are equal

ax 2 – (a 2 +1)∙x+ a= 0 = > x 1 = a x 2 = 1/a.

Example. Consider the equation 15x 2 –226x +15 = 0.

x 1 = 15 x 2 = 1/15.

3. If in Eq. ax 2 + bx – c = 0 coefficient “b” is equal to (a 2 – 1), and coefficient “c” is numerically equal to the coefficient “a”, then its roots are equal

ax 2 + (a 2 –1)∙x – a= 0 = > x 1 = – a x 2 = 1/a.

Example. Consider the equation 17x 2 +288x – 17 = 0.

x 1 = – 17 x 2 = 1/17.

4. If in the equation ax 2 – bx – c = 0 the coefficient “b” is equal to (a 2 – 1), and the coefficient c is numerically equal to the coefficient “a”, then its roots are equal

ax 2 – (a 2 –1)∙x – a= 0 = > x 1 = a x 2 = – 1/a.

Example. Consider the equation 10x 2 – 99x –10 = 0.

x 1 = 10 x 2 = – 1/10

Vieta's theorem.

Vieta's theorem is named after the famous French mathematician Francois Vieta. Using Vieta's theorem, we can express the sum and product of the roots of an arbitrary KU in terms of its coefficients.

45 = 1∙45 45 = 3∙15 45 = 5∙9.

In total, the number 14 gives only 5 and 9. These are roots. With a certain skill, using the presented theorem, you can solve many quadratic equations orally immediately.

Vieta's theorem, in addition. It is convenient in that after solving a quadratic equation in the usual way (through a discriminant), the resulting roots can be checked. I recommend doing this always.

TRANSPORTATION METHOD

With this method, the coefficient “a” is multiplied by the free term, as if “thrown” to it, which is why it is called "transfer" method. This method is used when the roots of the equation can be easily found using Vieta's theorem and, most importantly, when the discriminant is an exact square.

If A± b+c≠ 0, then the transfer technique is used, for example:

2X 2 – 11x+ 5 = 0 (1) => X 2 – 11x+ 10 = 0 (2)

Using Vieta's theorem in equation (2), it is easy to determine that x 1 = 10 x 2 = 1

The resulting roots of the equation must be divided by 2 (since the two were “thrown” from x 2), we get

x 1 = 5 x 2 = 0.5.

What is the rationale? Look what's happening.

The discriminants of equations (1) and (2) are equal:

If you look at the roots of the equations, you only get different denominators, and the result depends precisely on the coefficient of x 2:

The second (modified) one has roots that are 2 times larger.

Therefore, we divide the result by 2.

*If we reroll the three, we will divide the result by 3, etc.

Answer: x 1 = 5 x 2 = 0.5

Sq. ur-ie and Unified State Examination.

I’ll tell you briefly about its importance - YOU MUST BE ABLE TO DECIDE quickly and without thinking, you need to know the formulas of roots and discriminants by heart. Many of the problems included in the Unified State Examination tasks come down to solving a quadratic equation (geometric ones included).

Something worth noting!

1. The form of writing an equation can be “implicit”. For example, the following entry is possible:

15+ 9x 2 - 45x = 0 or 15x+42+9x 2 - 45x=0 or 15 -5x+10x 2 = 0.

You need to bring it to a standard form (so as not to get confused when solving).

2. Remember that x is an unknown quantity and it can be denoted by any other letter - t, q, p, h and others.

I hope that after studying this article you will learn how to find the roots of a complete quadratic equation.

Using the discriminant, only complete quadratic equations are solved; to solve incomplete quadratic equations, other methods are used, which you will find in the article “Solving incomplete quadratic equations.”

What quadratic equations are called complete? This equations of the form ax 2 + b x + c = 0, where coefficients a, b and c are not equal to zero. So, to solve a complete quadratic equation, we need to calculate the discriminant D.

D = b 2 – 4ac.

Depending on the value of the discriminant, we will write down the answer.

If the discriminant a negative number(D< 0),то корней нет.

If the discriminant is zero, then x = (-b)/2a. When the discriminant is a positive number (D > 0),

then x 1 = (-b - √D)/2a, and x 2 = (-b + √D)/2a.

For example. Solve the equation x 2– 4x + 4= 0.

D = 4 2 – 4 4 = 0

x = (- (-4))/2 = 2

Answer: 2.

Solve Equation 2 x 2 + x + 3 = 0.

D = 1 2 – 4 2 3 = – 23

Answer: no roots.

Solve Equation 2 x 2 + 5x – 7 = 0.

D = 5 2 – 4 2 (–7) = 81

x 1 = (-5 - √81)/(2 2)= (-5 - 9)/4= – 3.5

x 2 = (-5 + √81)/(2 2) = (-5 + 9)/4=1

Answer: – 3.5; 1.

So let’s imagine the solution of complete quadratic equations using the diagram in Figure 1.

Using these formulas you can solve any complete quadratic equation. You just need to be careful to the equation was written as a polynomial of the standard form

A x 2 + bx + c, otherwise you may make a mistake. For example, in writing the equation x + 3 + 2x 2 = 0, you can mistakenly decide that

a = 1, b = 3 and c = 2. Then

D = 3 2 – 4 1 2 = 1 and then the equation has two roots. And this is not true. (See solution to example 2 above).

Therefore, if the equation is not written as a polynomial of the standard form, first the complete quadratic equation must be written as a polynomial of the standard form (the monomial with the largest exponent should come first, that is A x 2 , then with less – bx and then a free member With.

When solving the above quadratic equation and a quadratic equation with an even coefficient in the second term, you can use other formulas. Let's get acquainted with these formulas. If in a complete quadratic equation the second term has an even coefficient (b = 2k), then you can solve the equation using the formulas shown in the diagram in Figure 2.

A complete quadratic equation is called reduced if the coefficient at x 2 is equal to one and the equation takes the form x 2 + px + q = 0. Such an equation can be given to solve, or it can be obtained by dividing all the coefficients of the equation by the coefficient A, standing at x 2 .

Figure 3 shows a diagram for solving the reduced square
equations. Let's look at an example of the application of the formulas discussed in this article.

Example. Solve the equation

3x 2 + 6x – 6 = 0.

Let's solve this equation using the formulas shown in the diagram in Figure 1.

D = 6 2 – 4 3 (– 6) = 36 + 72 = 108

√D = √108 = √(36 3) = 6√3

x 1 = (-6 - 6√3)/(2 3) = (6 (-1- √(3)))/6 = –1 – √3

x 2 = (-6 + 6√3)/(2 3) = (6 (-1+ √(3)))/6 = –1 + √3

Answer: –1 – √3; –1 + √3

You can notice that the coefficient of x in this equation is an even number, that is, b = 6 or b = 2k, whence k = 3. Then let’s try to solve the equation using the formulas shown in the diagram of the figure D 1 = 3 2 – 3 · (– 6 ) = 9 + 18 = 27

√(D 1) = √27 = √(9 3) = 3√3

x 1 = (-3 - 3√3)/3 = (3 (-1 - √(3)))/3 = – 1 – √3

x 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Answer: –1 – √3; –1 + √3. Noticing that all the coefficients in this quadratic equation are divisible by 3 and performing the division, we get the reduced quadratic equation x 2 + 2x – 2 = 0 Solve this equation using the formulas for the reduced quadratic
equations figure 3.

D 2 = 2 2 – 4 (– 2) = 4 + 8 = 12

√(D 2) = √12 = √(4 3) = 2√3

x 1 = (-2 - 2√3)/2 = (2 (-1 - √(3)))/2 = – 1 – √3

x 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Answer: –1 – √3; –1 + √3.

As you can see, when solving this equation using different formulas, we received the same answer. Therefore, having thoroughly mastered the formulas shown in the diagram in Figure 1, you will always be able to solve any complete quadratic equation.

blog.site, when copying material in full or in part, a link to the original source is required.