The formula for adding logarithms with the same base. Logarithmic Expressions

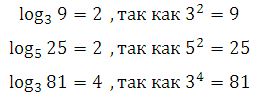
Logarithmic expressions, solution of examples. In this article, we will consider problems related to solving logarithms. The tasks raise the question of finding the value of the expression. It should be noted that the concept of the logarithm is used in many tasks and it is extremely important to understand its meaning. As for the USE, the logarithm is used in solving equations, in applied problems, and also in tasks related to the study of functions.

Here are examples to understand the very meaning of the logarithm:

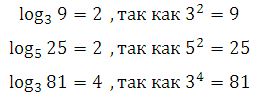
Basic logarithmic identity:

Properties of logarithms that you must always remember:

*The logarithm of the product is equal to the sum of the logarithms of the factors.

* * *

* The logarithm of the quotient (fraction) is equal to the difference of the logarithms of the factors.

* * *

* The logarithm of the degree is equal to the product of the exponent and the logarithm of its base.

* * *

*Transition to new base

* * *

More properties:

* * *

Computing logarithms is closely related to using the properties of exponents.

We list some of them:

The essence of this property is that when transferring the numerator to the denominator and vice versa, the sign of the exponent changes to the opposite. For instance:

Consequence of this property:

* * *

When raising a power to a power, the base remains the same, but the exponents are multiplied.

* * *

As you can see, the very concept of the logarithm is simple. The main thing is that good practice is needed, which gives a certain skill. Certainly knowledge of formulas is obligatory. If the skill in converting elementary logarithms is not formed, then when solving simple tasks, one can easily make a mistake.

Practice, solve the simplest examples from the math course first, then move on to more complex ones. In the future, I will definitely show how the “ugly” logarithms are solved, there will be no such ones at the exam, but they are of interest, do not miss it!

That's all! Good luck to you!

Sincerely, Alexander Krutitskikh

P.S: I would be grateful if you tell about the site in social networks.

274. Remarks.

a) If the expression to be evaluated contains sum or difference numbers, then they must be found without the help of tables by ordinary addition or subtraction. For example:

log (35 + 7.24) 5 = 5 log (35 + 7.24) = 5 log 42.24.

b) Knowing how to logarithm expressions, we can, inversely, from the given result of the logarithm, find the expression from which this result was obtained; so if

log X= log a+log b- 3 logs With,

it is easy to imagine that

v) Before proceeding to consider the structure of logarithmic tables, we will indicate some properties of decimal logarithms, i.e. those in which the number 10 is taken as the basis (only such logarithms are used for calculations).

Chapter two.

Properties of decimal logarithms.

275 . a) Since 10 1 = 10, 10 2 = 100, 10 3 = 1000, 10 4 = 10000, etc., then log 10 = 1, log 100 = 2, log 1000 = 3, log 10000 = 4, and etc.

Means, the logarithm of an integer represented by one with zeros is a positive integer containing as many ones as there are zeros in the image of the number.

In this way: log 100,000 = 5, log 1000 000 = 6 , etc.

b) Because

log 0.1 = -l; log 0.01 = - 2; log 0.001 == -3; log 0.0001 = - 4, etc.

Means, The logarithm of a decimal fraction, represented by a unit with leading zeros, is a negative integer containing as many negative units as there are zeros in the image of the fraction, including 0 integers.

In this way: log 0.00001= - 5, log 0.000001 = -6, etc.

v) Take an integer that is not represented by a unit with zeros, for example. 35, or an integer with a fraction, e.g. 10.7. The logarithm of such a number cannot be an integer, since by raising 10 to a power with an integer exponent (positive or negative), we get 1 with zeros (following or preceding 1). Suppose now that the logarithm of such a number is some fraction a / b . Then we would have equalities

But these equalities are impossible, as 10a is 1 with zeros, while powers 35b and 10,7b no indicator b cannot give 1 with zeros. Hence, it cannot be allowed log 35 and log 10.7 were equal to fractions. But from the properties of the logarithmic function, we know () that every positive number has a logarithm; therefore, each of the numbers 35 and 10.7 has its own logarithm, and since it cannot be either a whole number or a fractional number, it is an irrational number and, therefore, cannot be expressed exactly by means of numbers. Usually, irrational logarithms are expressed approximately as a decimal fraction with several decimal places. The integer of this fraction (even though it was "0 integers") is called characteristic, and the fractional part is the mantissa of the logarithm. If, for example, the logarithm is 1,5441 , then its characteristic is 1 , and the mantissa is 0,5441 .

G) Let's take some integer or mixed number, for example. 623 or 623,57 . The logarithm of such a number consists of a characteristic and a mantissa. It turns out that decimal logarithms have the convenience that we can always find their characteristic by one type of number . To do this, we count how many digits are in a given integer, or in the integer part of a mixed number. In our examples of these numbers 3 . Therefore, each of the numbers 623 and 623,57 more than 100 but less than 1000; which means that the logarithm of each of them is greater log 100, i.e. more 2 , but less log 1000, i.e. less 3 (remember that a larger number also has a larger logarithm). Hence, log 623 = 2,..., and log 623.57 = 2,... (points replace unknown mantissas).

Like this we find:

10 < 56,7 < 100 1 < log56,7 < 2 log 56,7 = 1,...

1000 < 8634 < 10 000 3 < log8634 < 4 log 8634 = 3,...

Let in general a given integer, or an integer part of a given mixed number, contain m digits. Since the smallest integer containing m digits, there 1 With m - 1 trailing zeros, then (denoting the given number N) we can write the inequalities:

and hence

m - 1 < log N < m ,

log N = ( m- 1) + positive fraction.

So the characteristic logN = m - 1 .

We see in this way that the characteristic of the logarithm of an integer or mixed number contains as many positive ones as there are digits in the integer part of the number without one.

With this in mind, we can directly write:

log 7,205 = 0,...; log83 = 1,...; log 720.4 = 2,... etc.

e) Let's take some decimal fractions smaller than 1 (i.e. having 0 integers): 0,35; 0,07; 0,0056; 0,0008, etc.

Thus, each of these logarithms is enclosed between two negative integers that differ by one; so each of them is equal to the smaller of these negative numbers increased by some positive fraction. For example, log0.0056= -3 + positive fraction. Suppose this fraction is 0.7482. Then, that means:

log 0.0056 = - 3 + 0.7482 (= - 2.2518).

Amounts such as - 3 + 0,7482 , consisting of a negative integer and a positive decimal fraction, agreed to write abbreviated in logarithmic calculations as follows: 3 ,7482 (Such a number reads: 3 with a minus, 7482 ten-thousandths.), i.e. put a minus sign over the characteristic in order to show that it refers only to this characteristic, and not to the mantissa, which remains positive. Thus, from the table above, it can be seen that

log 0.35 == 1 ,....; log 0.07 = 2 ,....; log 0.0008 = 4 ,....

Let at all . there is a decimal fraction in which the first significant digit α costs m zeros, including 0 integers. Then it is obvious that

- m < log A < - (m- 1).

Since out of two integers:- m and - (m- 1) there is less m , then

log A = - m+ positive fraction,

and therefore the characteristic log A = - m (with a positive mantissa).

In this way, the characteristic of the logarithm of a decimal fraction less than 1 contains as many negative ones as there are zeros in the image of the decimal fraction in front of the first significant digit, including zero integers; the mantissa of such a logarithm is positive.

e) Multiply some number N(whole or fractional - it doesn't matter) by 10, by 100 by 1000..., generally by 1 with zeros. Let's see how this changes log N. Since the logarithm of the product is equal to the sum of the logarithms of the factors, then

log(N 10) = log N + log 10 = log N + 1;

log(N 100) = log N + log 100 = log N + 2;

log(N 1000) = log N + log 1000 = log N + 3; etc.

When to log N we add some integer, then we can always add this number to the characteristic, and not to the mantissa.

So, if log N = 2.7804, then 2.7804 + 1 = 3.7804; 2.7804 + 2 = 4.7801 etc.;

or if log N = 3.5649, then 3.5649 + 1 = 2.5649; 3.5649 + 2 = 1.5649, etc.

From multiplying a number by 10, 100, 1000, .., generally by 1 with zeros, the mantissa of the logarithm does not change, and the characteristic increases by as many units as there are zeros in the multiplier .

Similarly, taking into account that the logarithm of the quotient is equal to the logarithm of the dividend without the logarithm of the divisor, we get:

log N / 10 = log N - log 10 = log N -1;

log N / 100 = log N - log 100 = log N -2;

log N / 1000 = log N - log 1000 = log N -3; etc.

If we agree, when subtracting an integer from the logarithm, to subtract this integer always from the characteristic, and leave the mantissa unchanged, then we can say:

From dividing a number by 1 with zeros, the mantissa of the logarithm does not change, and the characteristic decreases by as many units as there are zeros in the divisor.

276. Consequences. From property ( e) we can deduce the following two corollaries:

a) The mantissa of the logarithm of a decimal number does not change from being moved in the number by a comma , because moving a comma is equivalent to multiplying or dividing by 10, 100, 1000, etc. Thus, the logarithms of numbers:

0,00423, 0,0423, 4,23, 423

differ only in characteristics, but not in mantissas (provided that all mantissas are positive).

b) The mantissas of numbers that have the same significant part, but differ only by zeros at the end, are the same: so, the logarithms of numbers: 23, 230, 2300, 23,000 differ only in characteristics.

Comment. From these properties of decimal logarithms, it can be seen that we can find the characteristic of the logarithm of an integer and a decimal fraction without the help of tables (this is the great convenience of decimal logarithms); as a result, only one mantissa is placed in logarithmic tables; in addition, since finding the logarithms of fractions is reduced to finding the logarithms of integers (the logarithm of a fraction \u003d the logarithm of the numerator without the logarithm of the denominator), the mantissas of the logarithms of only integers are placed in the tables.

Chapter three.

The device and use of four-digit tables.

277. Systems of logarithms. A system of logarithms is a set of logarithms calculated for a series of consecutive integers in the same base. Two systems are used: the system of ordinary or decimal logarithms, in which the number is taken as the basis 10 , and the system of so-called natural logarithms, in which the irrational number is taken as the basis (for some reasons that are understood in other parts of mathematics) 2,7182818 ... For calculations, decimal logarithms are used, due to the conveniences that we indicated when we listed the properties of such logarithms.

Natural logarithms are also called Napier's logarithms after the inventor of logarithms, a Scottish mathematician. Nepera(1550-1617), and decimal logarithms - by Brigg named after professor brigga(a contemporary and friend of Napier), who first compiled tables of these logarithms.

278. Transformation of a negative logarithm into one with a positive mantissa, and inverse transformation. We have seen that the logarithms of numbers less than 1 are negative. Hence, they consist of a negative characteristic and a negative mantissa. Such logarithms can always be transformed so that their mantissa is positive, but the characteristic remains negative. To do this, it is enough to add a positive unit to the mantissa, and a negative unit to the characteristic (from which, of course, the value of the logarithm will not change).

If, for example, we have the logarithm - 2,0873 , then you can write:

- 2,0873 = - 2 - 1 + 1 - 0,0873 = - (2 + 1) + (1 - 0,0873) = - 3 + 0,9127,

or abbreviated:

Conversely, any logarithm with a negative characteristic and a positive mantissa can be turned into a negative one. To do this, it is enough to attach a negative unit to a positive mantissa, and a positive one to a negative characteristic: so, you can write:

279. Description of four-digit tables. For solving most practical problems, four-digit tables are quite sufficient, the handling of which is very simple. These tables (with their "logarithms" at the top) are placed at the end of this book, and a small part of them (to explain the location) is printed on this page. They contain mantissas

Logarithms.

logarithms of all integers from 1 before 9999 inclusive, computed to four decimal places, the last of these places being increased by 1 in all those cases where the 5th decimal place would have to be 5 or more than 5; therefore, 4-digit tables give approximate mantissas up to 1 / 2 ten-thousandth part (with a deficiency or with an excess).

Since we can directly characterize the logarithm of an integer or a decimal fraction, based on the properties of decimal logarithms, we must take only the mantissa from the tables; at the same time, it must be remembered that the position of the comma in a decimal number, as well as the number of zeros at the end of the number, do not affect the value of the mantissa. Therefore, when finding the mantissa for a given number, we discard the comma in this number, as well as the zeros at the end of it, if any, and find the mantissa of the integer formed after this. In this case, the following cases may arise.

1) An integer consists of 3 digits. For example, let's find the mantissa of the logarithm of the number 536. The first two digits of this number, i.e. 53, are found in the tables in the first vertical column on the left (see table). Having found the number 53, we move from it along the horizontal line to the right until this line intersects with a vertical column passing through one of the numbers 0, 1, 2, 3, ... 9, set at the top (and bottom) of the table, which represents 3- th digit of this number, i.e. in our example, the number 6. At the intersection we get the mantissa 7292 (i.e. 0.7292), which belongs to the logarithm of the number 536. Similarly, for the number 508 we find the mantissa 0.7059, for the number 500 we find 0.6990 etc.

2) An integer consists of 2 or 1 digit. Then we mentally assign one or two zeros to this number and find the mantissa for the three-digit number thus formed. For example, we assign one zero to the number 51, from which we get 510 and find the mantissa 7070; we assign 2 zeros to the number 5 and find the mantissa 6990, etc.

3) An integer is expressed with 4 digits. For example, you need to find the mantissa of log 5436. Then first we find in the tables, as was just indicated, the mantissa for the number shown by the first 3 digits of this number, i.e. for 543 (this mantissa will be 7348); then we move from the found mantissa along the horizontal line to the right (to the right side of the table, located behind the thick vertical line) until the intersection with the vertical column passing through one of the numbers: 1, 2 3, ... 9, standing at the top (and at the bottom ) of this part of the table, which represents the 4th digit of a given number, i.e., in our example, the number 6. At the intersection we find the correction (number 5), which must be applied in the mind to the mantissa 7348 to get the mantissa of the number 5436; we will thus obtain a mantissa of 0.7353.

4) An integer is expressed with 5 or more digits. Then we discard all the digits, except for the first 4, and take an approximate four-digit number, and increase the last digit of this number by 1 in that. the case when the discarded 5th digit of the number is 5 or more than 5. So, instead of 57842 we take 5784, instead of 30257 we take 3026, instead of 583263 we take 5833, etc. For this rounded four-digit number, we find the mantissa as it has now been explained.

Guided by these instructions, we will find, for example, the logarithms of the following numbers:

36,5; 804,7; 0,26; 0,00345; 7,2634; 3456,06.

First of all, without referring to the tables for now, let's put down some characteristics, leaving room for the mantissas, which we write out after:

log 36.5 = 1,.... log 0.00345 = 3 ,....

log 804.7 = 2,.... log 7.2634 = 0,....

log 0.26 = 1 ,.... log 3456.86 = 3,....

log 36.5 = 1.5623; log 0.00345 = 3.5378;

log 804.7 = 2.9057; log 7.2634 = 0.8611;

log 0.26 = 1.4150; log 3456.86 = 3.5387.

280. Remark. In some four-digit tables (for example, in tables V. Lorchenko and N. Ogloblin, S. Glazenap, N. Kamenshchikova) corrections for the 4th digit of this number are not placed. When dealing with such tables, these corrections have to be found using a simple calculation, which can be performed on the basis of the following truth: if the numbers are greater than 100, and the differences between them are less than 1, then without sensitive error it can be assumed that the differences between the logarithms are proportional to the differences between the corresponding numbers . Let, for example, we need to find the mantissa corresponding to the number 5367. This mantissa, of course, is the same as for the number 536.7. We find the mantissa 7292 in the tables for the number 536. Comparing this mantissa with the mantissa 7300 adjacent to the right, corresponding to the number 537, we notice that if the number 536 increases by 1, then its mantissa will increase by 8 ten-thousandths (8 is the so-called tabular difference between two adjacent mantissas); if the number 536 increases by 0.7, then its mantissa will increase not by 8 ten-thousandths, but by some smaller number X ten-thousandths, which, according to the allowed proportionality, must satisfy the proportion:

X :8=0.7:1; where X = 8 07 = 5,6,

which is rounded to 6 ten-thousandths. This means that the mantissa for the number 536.7 (and therefore for the number 5367) will be: 7292 + 6 = 7298.

Note that finding an intermediate number by two adjacent numbers in the tables is called interpolation. The interpolation described here is called proportional, since it is based on the assumption that the change in the logarithm is proportional to the change in the number. It is also called linear, since it assumes that graphically the change in the logarithmic function is expressed by a straight line.

281. Limit of error of the approximate logarithm. If the number whose logarithm is being sought is an exact number, then for the error limit of its logarithm found in 4-digit tables, we can, as we said in, take 1 / 2 ten thousandth share. If the given number is not exact, then to this margin of error, one must also add the limit of another error arising from the inaccuracy of the number itself. It is proved (we omit this proof) that for such a limit one can take the product

a(d +1) ten thousandths.,

in which a is the margin of error of the most inexact number, assuming that 3 digits are taken in its integer part, a d tabular difference of the mantissas corresponding to two consecutive three-digit numbers between which this inexact number is enclosed. Thus, the limit of the final error of the logarithm will then be expressed by the formula:

1 / 2 + a(d +1) ten thousandth

Example. Find log π , taking for π approximate number 3.14, accurate to 1 / 2 hundredth.

By moving the comma after the 3rd digit in the number 3.14, counting from the left, we get the three-digit number 314, exact up to 1 / 2 units; this means that the margin of error of an inexact number, i.e., what we denoted by the letter a , if 1 / 2 From the tables we find:

log 3.14 = 0.4969.

Tabular difference d between the mantissas of the numbers 314 and 315 is 14, so the error of the found logarithm will be less

1 / 2 + 1 / 2 (14 +1) = 8 ten-thousandths.

Since we do not know about the logarithm of 0.4969 whether it is under or over, we can only guarantee that the exact logarithm π is between 0.4969 - 0.0008 and 0.4969 + 0.0008, i.e. 0.4961< log π < 0,4977.

282. Find a number from a given logarithm. To find a number according to a given logarithm, the same tables can be used, according to which the mantissas of these numbers are found; but it is more convenient to use other tables in which the so-called antilogarithms are placed, that is, numbers corresponding to given mantissas. These tables, labeled "antilogarithms" at the top, are placed at the end of this book, following the tables of logarithms; a small part of them is placed on this page (for explanation).

Let a 4-digit mantissa 2863 be given (we do not pay attention to the characteristic) and it is required to find the corresponding integer. Then, having tables of antilogarithms, we must use them in exactly the same way as was previously explained for finding the mantissa for a given number, namely: we find the first 2 digits of the mantissa in the first left column. Then we move from these numbers along the horizontal line to the right until the intersection with the vertical column coming from the 3rd digit of the mantissa, which must be searched for in the top line (or bottom). At the intersection we find the four-digit number 1932, corresponding to the mantissa 286. Then from this number we move further along the horizontal line to the right until the intersection with the vertical column coming from the 4th digit of the mantissa, which must be found at the top (or bottom) among the numbers 1, 2 put there , 3,... 9. At the intersection, we find the correction 1, which must be applied (in the mind) to the number 1032 found earlier in order to get the number corresponding to the mantissa of 2863.

Thus, the number will be 1933. After that, paying attention to the characteristic, it is necessary to put the occupied one in the proper place in the number 1933. For instance:

if log x = 3.2863, then X = 1933,

„ log x= 1,2863, „ X = 19,33,

, log x = 0,2&63, „ X = 1,933,

„ log x = 2 ,2863, „ X = 0,01933

Here are more examples:

log x = 0,2287, X = 1,693,

log x = 1 ,7635, X = 0,5801,

log x = 3,5029, X = 3184,

log x = 2 ,0436, X = 0,01106.

If the mantissa contains 5 or more digits, then we take only the first 4 digits, discarding the rest (and increasing the 4th digit by 1 if the 5th digit is five or more). For example, instead of mantissa 35478 we take 3548, instead of 47562 we take 4756.

283. Remark. The correction for the 4th and next digits of the mantissa can also be found by interpolation. So, if the mantissa is 84357, then, having found the number 6966 corresponding to the mantissa 843, we can reason further as follows: if the mantissa increases by 1 (thousandth), i.e., 844 is done, then the number, as can be seen from the tables, will increase by 16 units; if the mantissa increases not by 1 (thousandth), but by 0.57 (thousandth), then the number will increase by X units, and X should satisfy the proportions:

X : 16 = 0.57: 1, whence x = 16 0,57 = 9,12.

This means that the desired number will be 6966 + 9.12 = 6975.12 or (limited to only four digits) 6975.

284. Limit of error of the found number. It is proved that in the case when in the found number the comma is after the 3rd digit from the left, i.e. when the characteristic of the logarithm is 2, the sum can be taken as the margin of error

where a is the margin of error of the logarithm (expressed in ten-thousandths) by which the number was found, and d - the difference between the mantissas of two three-digit consecutive numbers between which the found number is enclosed (with a comma after the 3rd digit from the left). When the characteristic is not 2, but some other, then in the found number the comma will have to be moved to the left or right, i.e., divide or multiply the number by a certain power of 10. In this case, the error of the result will also be divided or multiplied by the same power of 10.

Let, for example, we find a number by the logarithm 1,5950 , which is known to be accurate to 3 ten-thousandths; so then a = 3 . The number corresponding to this logarithm, found from the table of antilogarithms, is 39,36 . Moving the comma after the 3rd digit on the left, we will have a number 393,6 between 393 and 394 . From the tables of logarithms, we see that the difference between the mantissas corresponding to these two numbers is 11 ten-thousandths; means d = 11 . The error of the number 393.6 will be less

So the number error 39,36 will be less 0,05 .

285. Actions on logarithms with negative characteristics. Adding and subtracting logarithms does not present any difficulties, as can be seen from the following examples:

There is also no difficulty in multiplying the logarithm by a positive number, for example:

In the last example, the positive mantissa is separately multiplied by 34, then the negative characteristic is multiplied by 34.

If the logarithm of a negative characteristic and a positive mantissa is multiplied by a negative number, then they act in two ways: either the previously given logarithm is turned negative, or the mantissa and characteristic are multiplied separately and the results are combined together, for example:

3 ,5632 (- 4) = - 2,4368 (- 4) = 9,7472;

3 ,5632 (- 4) = + 12 - 2,2528 = 9,7472.

When dividing, there are two cases: 1) the negative characteristic is divided and 2) is not divisible by a divisor. In the first case, the characteristic and mantissa are separated separately:

10 ,3784: 5 = 2 ,0757.

In the second case, so many negative units are added to the characteristic so that the resulting number is divisible by a divisor; the same number of positive units are added to the mantissa:

3 ,7608: 8 = (- 8 + 5,7608) : 8 = 1 ,7201.

This transformation must be done in the mind, so the action is arranged like this:

286. Replacing subtracted logarithms by terms. When calculating some complex expression using logarithms, you have to add some logarithms, subtract others; in this case, in the usual way of performing actions, they find separately the sum of the terms of the logarithms, then the sum of the subtracted ones, and subtract the second from the first sum. For example, if we have:

log X = 2,7305 - 2 ,0740 + 3 ,5464 - 8,3589 ,

then the usual execution of actions will be located like this:

However, it is possible to replace subtraction with addition. So:

Now you can arrange the calculation like this:

287. Examples of calculations.

Example 1. Evaluate expression:

if A \u003d 0.8216, B \u003d 0.04826, C \u003d 0.005127 and D = 7.246.

We logarithm this expression:

log X= 1/3 log A + 4 log B - 3 log C - 1/3 log D

Now, in order to avoid unnecessary loss of time and to reduce the possibility of errors, we first of all arrange all the calculations without executing them yet and without referring, therefore, to tables:

After that, we take the tables and put down the logarithms in the left empty places:

Limit of error. First, let's find the error limit of the number x 1 = 194,5 , equal to:

So, first of all, you need to find a , i.e., the margin of error of the approximate logarithm, expressed in ten-thousandths. Let's assume that these numbers A, B, C and D all are accurate. Then the errors in individual logarithms will be as follows (in ten-thousandths):

v logA.......... 1 / 2

v 1/3 log A......... 1 / 6 + 1 / 2 = 2 / 3

( 1 / 2 added because when dividing by 3 logarithms of 1.9146, we rounded the quotient by discarding its 5th digit, and, therefore, made another error, less 1 / 2 ten thousandth).

Now we find the margin of error of the logarithm:

a = 2 / 3 + 2 + 3 / 2 + 1 / 6 = 4 1 / 3 (ten thousandths).

Let us define further d . Because x 1 = 194,5 , then 2 consecutive integers between which is x 1 will 194 and 195 . Tabular difference d between the mantissas corresponding to these numbers is equal to 22 . So the margin of error of the number x 1 there is:

Because x = x 1 : 10, then the margin of error in the number x equals 0,3:10 = 0,03 . Thus, the number we found 19,45 differs from the exact number by less than 0,03 . Since we do not know whether our approximation has been found with a deficiency or with an excess, we can only guarantee that

19,45 + 0,03 > X > 19,45 - 0,03 , i.e.

19,48 > X > 19,42 ,

and therefore, if we accept X =19,4 , then we will have an approximation with a disadvantage up to 0.1.

Example 2 Calculate:

X = (- 2,31) 3 5 √72 = - (2,31) 3 5 √72 .

Since negative numbers do not have logarithms, we first find:

X" = (2,31) 3 5 √72

by decomposition:

log X"= 3 log 2.31 + 1/5 log72.

After the calculation will be:

X" = 28,99 ;

hence,

x = - 28,99 .

Example 3. Calculate:

A continuous logarithm cannot be applied here, since under the sign of the root stands with y m m a. In such cases, the formula is calculated in parts.

First we find N = 5 √8 , Then N 1 = 4 √3 ; Then, by simple addition, we determine N+ N 1 , and finally calculate 3 √N+ N 1 ; will turn out:

N = 1.514, N 1 = 1,316 ; N+ N 1 = 2,830 .

log x= log 3 √ 2,830 = 1 / 3 log 2,830 = 0,1506 ;

x = 1,415 .

Chapter Four.

Exponential and logarithmic equations.

288. An exponential equation is one in which the unknown is included in the exponent, and logarithmic- those in which the unknown enters under the sign log. Such equations can be solved only in special cases, and one has to rely on the properties of logarithms and on the principle that if the numbers are equal, then their logarithms are equal, and, conversely, if the logarithms are equal, then the corresponding numbers are equal.

Example 1 Solve the equation: 2 x = 1024 .

We logarithm both sides of the equation:

Example 2 Solve the equation: a 2x - a x = 1 . Putting a x = at , we get a quadratic equation:

y 2 - at - 1 = 0 ,

Because 1-√5 < 0 , then the last equation is impossible (function a x there is always a positive number), and the first gives:

Example 3 Solve the equation:

log( a + x) + log ( b + x) = log ( c + x) .

The equation can be written like this:

log[( a + x) (b + x)] = log ( c + x) .

From the equality of logarithms we conclude about the equality of numbers:

(a + x) (b + x) = c + x .

This is a quadratic equation, the solution of which is not difficult.

Chapter five.

Compound interest, term payments and urgent contributions.

289. The main problem for compound interest. What is the amount of capital a rubles, given in growth by R compound interest after t years ( t is an integer)?

It is said that capital is given out at compound interest, if the so-called "interest on interest" is taken into account, that is, if the interest money due on capital is added to the capital at the end of each year in order to increase it with interest in subsequent years.

Each ruble of capital given over R %, within one year will bring profit p / 100 ruble, and, consequently, each ruble of capital in 1 year will turn into 1 + p / 100 ruble (for example, if the capital is given for 5 %, then each ruble in a year will turn into 1 + 5 / 100 , i.e. in 1,05 ruble).

Denoting for brevity the fraction p / 100 one letter, for example, r , we can say that every ruble of capital in a year will turn into 1 + r rubles; hence, a rubles will turn in 1 year into a (1 + r ) rub. A year later, i.e., 2 years after the start of growth, each ruble of these a (1 + r ) rub. will turn back to 1 + r rub.; This means that all capital will be converted into a (1 + r ) 2 rub. In the same way we find that after three years the capital will be a (1 + r ) 3 , in four years will be a (1 + r ) 4 ,... in general through t years if t is an integer, it will turn into a (1 + r ) t rub. Thus, denoting A final capital, we will have the following compound interest formula:

A = a (1 + r ) t where r = p / 100 .

Example. Let a =2 300 rubles, p = 4, t=20 years; then the formula gives:

r = 4 / 100 = 0,04 ; A \u003d 2 300 (1.04) 20.

To calculate A, we use logarithms:

log a = log 2 300 + 20 log 1.04 = 3.3617 + 20 0.0170 = 3.3617+0.3400 = 3.7017.

A=5031 ruble.

Comment. In this example, we had log 1.04 multiply by 20 . Since the number 0,0170 there is an approximation log 1.04 up to 1 / 2 ten-thousandth part, then the product of this number by 20 will only be until 1 / 2 20, i.e. up to 10 ten-thousandths \u003d 1 thousandth. Therefore, in total 3,7017 we cannot vouch for not only the figure of ten-thousandths, but also the figure of thousandths. In order to obtain greater accuracy in such cases, it is better for the number 1 + r take logarithms not 4-digit, but with a large number of digits, for example. 7 digits. For this purpose, we provide here a small table in which 7-digit logarithms are written out for the most common values. R .

290. The main task for urgent payments. Someone took a rubles for R % with the condition to repay the debt, together with the interest due on it, in t years, paying the same amount at the end of each year. What should this amount be?

Sum x paid annually under such conditions is called urgent payment. Let's again denote r annual interest money from 1 ruble, that is, the number p / 100 . Then by the end of the first year the debt a rises to a (1 + r ), after payment X rubles it will be done a (1 + r )-X .

By the end of the second year, each ruble of this amount will again turn into 1 + r rubles, and therefore the debt will be [ a (1 + r )-X ](1 + r ) = a (1 + r ) 2 - x (1 + r ), and for payment x rubles will be: a (1 + r ) 2 - x (1 + r ) - X . In the same way, we will make sure that by the end of the 3rd year the debt will be

a (1 + r ) 3 - x (1 + r ) 2 - x (1 + r ) - x ,

and in general and the end t -th year it will be:

a (1 + r ) t - x (1 + r ) t-1 - x (1 + r ) t-2 ... - x (1 + r ) - x , or

a (1 + r ) t - x [ 1 + (1 + r ) + (1 + r ) 2 + ...+ (1 + r ) t-2 + (1 + r ) t-1 ]

The polynomial inside the brackets represents the sum of the terms of the geometric progression; which has the first member 1 , last ( 1 + r ) t-1, and the denominator ( 1 + r ). According to the formula for the sum of members of a geometric progression (section 10 chapter 3 § 249) we find:

and the amount of debt after t -th payment will be:

According to the condition of the problem, the debt at the end t -th year should be equal to 0 ; That's why:

where

When calculating this urgent payment formulas using logarithms, we must first find an auxiliary number N = (1 + r ) t by logarithm: logN= t log (1 + r) ; finding N, subtract 1 from it, then we get the denominator of the formula for X, after which, by the secondary logarithm, we find:

log X= log a+ log N + log r - log (N - 1).

291. Main task for urgent contributions. Someone deposits the same amount into the bank at the beginning of each year a rub. Determine what capital is formed from these contributions after t years if the bank pays R compound interest.

Denoting through r annual interest money from 1 ruble, i.e. p / 100 , we argue as follows: by the end of the first year, the capital will a (1 + r );

at the beginning of the 2nd year, this amount will be added a rubles; This means that at this time the capital will be a (1 + r ) + a . By the end of year 2, he will a (1 + r ) 2 + a (1 + r );

at the beginning of the 3rd year is again introduced a rubles; This means that at this time the capital will be a (1 + r ) 2 + a (1 + r ) + a ; by the end of the 3rd he will be a (1 + r ) 3 + a (1 + r ) 2 + a (1 + r ) Continuing these considerations further, we find that by the end t year required capital A will:

This is the formula for fixed-term contributions made at the beginning of each year.

The same formula can be obtained by the following reasoning: first installment in a rubles while in the bank t years, will turn, according to the compound interest formula, into a (1 + r ) t rub. The second installment, being in the bank one year less, i.e. t - 1 years, contact a (1 + r ) t-1 rub. Similarly, the third installment will give a (1 + r ) t-2 etc., and finally, the last installment, being in the bank for only 1 year, will turn to a (1 + r ) rub. So the final capital A rub. will:

A= a (1 + r ) t + a (1 + r ) t-1 + a (1 + r ) t-2 + . . . + a (1 + r ),

which, after simplification, gives the formula found above.

When calculating using the logarithms of this formula, you must do the same as when calculating the formula for urgent payments, i.e., first find the number N = ( 1 + r ) t according to its logarithm: logN= t log(1 + r ), then a number N-1 and then take the logarithm of the formula:

log A = log a+ log (1 + r) + log (N - 1) - 1ogr

Comment. If the urgent contribution to a rub. was made not at the beginning, but at the end of each year (as, for example, an urgent payment is made X to repay the debt), then, arguing like the previous one, we find that by the end t year required capital A" rub. will be (including the last installment a rub., not bearing interest):

A"= a (1 + r ) t-1 + a (1 + r ) t-2 + . . . + a (1 + r ) + a

which is equal to:

i.e. A" appears in ( 1 + r ) times less A, which was to be expected, since each ruble of capital A" lies in the bank for a year less than the corresponding ruble of capital A.

Your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please read our privacy policy and let us know if you have any questions.

Collection and use of personal information

Personal information refers to data that can be used to identify or contact a specific person.

You may be asked to provide your personal information at any time when you contact us.

The following are some examples of the types of personal information we may collect and how we may use such information.

What personal information we collect:

• When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.

How we use your personal information:

• The personal information we collect allows us to contact you and inform you about unique offers, promotions and other events and upcoming events.
• From time to time, we may use your personal information to send you important notices and communications.
• We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
• If you enter a prize draw, contest or similar incentive, we may use the information you provide to administer such programs.

Disclosure to third parties

We do not disclose information received from you to third parties.

Exceptions:

• In the event that it is necessary - in accordance with the law, judicial order, in legal proceedings, and / or based on public requests or requests from state bodies in the territory of the Russian Federation - disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public interest reasons.
• In the event of a reorganization, merger or sale, we may transfer the personal information we collect to the relevant third party successor.

Protection of personal information

We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as from unauthorized access, disclosure, alteration and destruction.

Maintaining your privacy at the company level

To ensure that your personal information is secure, we communicate privacy and security practices to our employees and strictly enforce privacy practices.

1. Check if there are negative numbers or one under the logarithm sign. This method is applicable to expressions of the form log b ⁡ (x) log b ⁡ (a) (\displaystyle (\frac (\log _(b)(x))(\log _(b)(a)))). However, it is not suitable for some special cases:

   • The logarithm of a negative number is not defined in any base (for example, log ⁡ (− 3) (\displaystyle \log(-3)) or log 4 ⁡ (− 5) (\displaystyle \log _(4)(-5))). In this case, write "no solution".
   • The logarithm of zero to any base is also undefined. If you got caught ln ⁡ (0) (\displaystyle \ln(0)), write "no solution".
   • The logarithm of unity in any base ( log ⁡ (1) (\displaystyle \log(1))) is always zero because x 0 = 1 (\displaystyle x^(0)=1) for all values x. Write instead of such a logarithm 1 and do not use the method below.
   • If the logarithms have different bases, for example l o g 3 (x) l o g 4 (a) (\displaystyle (\frac (log_(3)(x))(log_(4)(a)))), and are not reduced to integers, the value of the expression cannot be found manually.

2. Convert the expression to one logarithm. If the expression does not apply to the above special cases, it can be represented as a single logarithm. Use the following formula for this: log b ⁡ (x) log b ⁡ (a) = log a ⁡ (x) (\displaystyle (\frac (\log _(b)(x))(\log _(b)(a)))=\ log_(a)(x)).

   • Example 1: consider the expression log ⁡ 16 log ⁡ 2 (\displaystyle (\frac (\log (16))(\log (2)))).
     First, let's represent the expression as a single logarithm using the above formula: log ⁡ 16 log ⁡ 2 = log 2 ⁡ (16) (\displaystyle (\frac (\log (16))(\log (2)))=\log _(2)(16)).
   • This "change of base" formula for the logarithm is derived from the basic properties of logarithms.

3. If possible, calculate the value of the expression manually. To find log a ⁡ (x) (\displaystyle \log _(a)(x)), imagine the expression " a? = x (\displaystyle a^(?)=x)", that is, ask the following question:" To what power it is necessary to raise a, To obtain x?". This question may require a calculator, but if you're lucky, you can find it manually.

   • Example 1 (continued): Rewrite as 2? = 16 (\displaystyle 2^(?)=16). It is necessary to find what number should stand instead of the sign "?". This can be done by trial and error:
     2 2 = 2 ∗ 2 = 4 (\displaystyle 2^(2)=2*2=4)
     2 3 = 4 ∗ 2 = 8 (\displaystyle 2^(3)=4*2=8)
     2 4 = 8 ∗ 2 = 16 (\displaystyle 2^(4)=8*2=16)
     So, the desired number is 4: log 2 ⁡ (16) (\displaystyle \log _(2)(16)) = 4 .

4. Leave the answer in logarithmic form if you can't simplify it. Many logarithms are very difficult to calculate by hand. In this case, you will need a calculator to get an accurate answer. However, if you are solving a problem in class, then the teacher will most likely be satisfied with the answer in logarithmic form. The method below is used to solve a more complex example:

   • example 2: what is equal log 3 ⁡ (58) log 3 ⁡ (7) (\displaystyle (\frac (\log _(3)(58))(\log _(3)(7))))?
   • Let's convert this expression to one logarithm: log 3 ⁡ (58) log 3 ⁡ (7) = log 7 ⁡ (58) (\displaystyle (\frac (\log _(3)(58))(\log _(3)(7)))=\ log_(7)(58)). Note that the base 3 common to both logarithms disappears; this is true for any base.
   • Let's rewrite the expression in the form 7? = 58 (\displaystyle 7^(?)=58) and try to find the value?:
     7 2 = 7 ∗ 7 = 49 (\displaystyle 7^(2)=7*7=49)
     7 3 = 49 ∗ 7 = 343 (\displaystyle 7^(3)=49*7=343)
     Since 58 is between these two numbers, it is not expressed as a whole number.
   • We leave the answer in logarithmic form: log 7 ⁡ (58) (\displaystyle \log _(7)(58)).

So, we have powers of two. If you take the number from the bottom line, then you can easily find the power to which you have to raise a two to get this number. For example, to get 16, you need to raise two to the fourth power. And to get 64, you need to raise two to the sixth power. This can be seen from the table.

And now - in fact, the definition of the logarithm:

The logarithm to the base a of the argument x is the power to which the number a must be raised to get the number x .

Notation: log a x \u003d b, where a is the base, x is the argument, b is actually what the logarithm is equal to.

For example, 2 3 = 8 ⇒ log 2 8 = 3 (the base 2 logarithm of 8 is three because 2 3 = 8). Might as well log 2 64 = 6 because 2 6 = 64 .

The operation of finding the logarithm of a number to a given base is called the logarithm. So let's add a new row to our table:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
log 2 2 = 1	log 2 4 = 2	log 2 8 = 3	log 2 16 = 4	log 2 32 = 5	log 2 64 = 6

Unfortunately, not all logarithms are considered so easily. For example, try to find log 2 5 . The number 5 is not in the table, but logic dictates that the logarithm will lie somewhere on the segment. Because 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

Such numbers are called irrational: the numbers after the decimal point can be written indefinitely, and they never repeat. If the logarithm turns out to be irrational, it is better to leave it like this: log 2 5 , log 3 8 , log 5 100 .

It is important to understand that the logarithm is an expression with two variables (base and argument). At first, many people confuse where the base is and where the argument is. To avoid annoying misunderstandings, just take a look at the picture:

Before us is nothing more than the definition of the logarithm. Remember: the logarithm is the power, to which you need to raise the base to get the argument. It is the base that is raised to a power - in the picture it is highlighted in red. It turns out that the base is always at the bottom! I tell this wonderful rule to my students at the very first lesson - and there is no confusion.

We figured out the definition - it remains to learn how to count logarithms, i.e. get rid of the "log" sign. To begin with, we note that two important facts follow from the definition:

1. The argument and base must always be greater than zero. This follows from the definition of the degree by a rational exponent, to which the definition of the logarithm is reduced.
2. The base must be different from unity, since a unit to any power is still a unit. Because of this, the question “to what power must one be raised to get two” is meaningless. There is no such degree!

Such restrictions are called valid range(ODZ). It turns out that the ODZ of the logarithm looks like this: log a x = b ⇒ x > 0 , a > 0 , a ≠ 1 .

Note that there are no restrictions on the number b (the value of the logarithm) is not imposed. For example, the logarithm may well be negative: log 2 0.5 \u003d -1, because 0.5 = 2 −1 .

However, now we are considering only numerical expressions, where it is not required to know the ODZ of the logarithm. All restrictions have already been taken into account by the compilers of the problems. But when logarithmic equations and inequalities come into play, the DHS requirements will become mandatory. Indeed, in the basis and argument there can be very strong constructions that do not necessarily correspond to the above restrictions.

Now consider the general scheme for calculating logarithms. It consists of three steps:

1. Express the base a and the argument x as a power with the smallest possible base greater than one. Along the way, it is better to get rid of decimal fractions;
2. Solve the equation for the variable b: x = a b ;
3. The resulting number b will be the answer.

That's all! If the logarithm turns out to be irrational, this will be seen already at the first step. The requirement that the base be greater than one is very relevant: this reduces the likelihood of error and greatly simplifies calculations. Similarly with decimal fractions: if you immediately convert them to ordinary ones, there will be many times less errors.

Let's see how this scheme works with specific examples:

Task. Calculate the logarithm: log 5 25

1. Let's represent the base and the argument as a power of five: 5 = 5 1 ; 25 = 52;

Let's make and solve the equation:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2 ;

2. Received an answer: 2.

Task. Calculate the logarithm:

Task. Calculate the logarithm: log 4 64

1. Let's represent the base and the argument as a power of two: 4 = 2 2 ; 64 = 26;
2. Let's make and solve the equation:
   log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ;
3. Received an answer: 3.

Task. Calculate the logarithm: log 16 1

1. Let's represent the base and the argument as a power of two: 16 = 2 4 ; 1 = 20;
2. Let's make and solve the equation:
   log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ;
3. Received a response: 0.

Task. Calculate the logarithm: log 7 14

1. Let's represent the base and the argument as a power of seven: 7 = 7 1 ; 14 is not represented as a power of seven, because 7 1< 14 < 7 2 ;
2. It follows from the previous paragraph that the logarithm is not considered;
3. The answer is no change: log 7 14.

A small note on the last example. How to make sure that a number is not an exact power of another number? Very simple - just decompose it into prime factors. If there are at least two distinct factors in the expansion, the number is not an exact power.

Task. Find out if the exact powers of the number are: 8; 48; 81; 35; 14 .

8 \u003d 2 2 2 \u003d 2 3 - the exact degree, because there is only one multiplier;
48 = 6 8 = 3 2 2 2 2 = 3 2 4 is not an exact power because there are two factors: 3 and 2;
81 \u003d 9 9 \u003d 3 3 3 3 \u003d 3 4 - exact degree;
35 = 7 5 - again not an exact degree;
14 \u003d 7 2 - again not an exact degree;

Note also that the prime numbers themselves are always exact powers of themselves.

Decimal logarithm

Some logarithms are so common that they have a special name and designation.

The decimal logarithm of the x argument is the base 10 logarithm, i.e. the power to which you need to raise the number 10 to get the number x. Designation: lg x .

For example, log 10 = 1; log 100 = 2; lg 1000 = 3 - etc.

From now on, when a phrase like “Find lg 0.01” appears in the textbook, know that this is not a typo. This is the decimal logarithm. However, if you are not used to such a designation, you can always rewrite it:
log x = log 10 x

Everything that is true for ordinary logarithms is also true for decimals.

natural logarithm

There is another logarithm that has its own notation. In a sense, it is even more important than decimal. This is the natural logarithm.

The natural logarithm of x is the base e logarithm, i.e. the power to which the number e must be raised to obtain the number x. Designation: ln x .

Many will ask: what else is the number e? This is an irrational number, its exact value cannot be found and written down. Here are just the first numbers:
e = 2.718281828459...

We will not delve into what this number is and why it is needed. Just remember that e is the base of the natural logarithm:
ln x = log e x

Thus ln e = 1 ; log e 2 = 2 ; ln e 16 = 16 - etc. On the other hand, ln 2 is an irrational number. In general, the natural logarithm of any rational number is irrational. Except, of course, unity: ln 1 = 0.

For natural logarithms, all the rules that are true for ordinary logarithms are valid.