Function extremes. How to find the largest value of a function on an interval

And to solve it, you need minimal knowledge of the topic. The next academic year is ending, everyone wants to go on vacation, and in order to bring this moment closer, I immediately get down to business:

Let's start with the area. The area referred to in the condition is limited closed set of points in the plane. For example, a set of points bounded by a triangle, including the ENTIRE triangle (if from borders“Poke out” at least one point, then the area will no longer be closed). In practice, there are also areas of rectangular, round and slightly more complex shapes. It should be noted that in the theory of mathematical analysis, strict definitions are given limitations, isolation, boundaries, etc., but I think everyone is aware of these concepts on an intuitive level, and more is not needed now.

The flat area is standardly denoted by the letter , and, as a rule, is given analytically - by several equations (not necessarily linear); less often inequalities. A typical verbal turnover: "closed arealimited by lines".

An integral part of the task under consideration is the construction of the area on the drawing. How to do it? It is necessary to draw all the listed lines (in this case 3 straight) and analyze what happened. The desired area is usually lightly hatched, and its border is highlighted with a bold line:


The same area can be set linear inequalities: , which for some reason are more often written as an enumeration list, and not system.
Since the boundary belongs to the region, then all inequalities, of course, non-strict.

And now the crux of the matter. Imagine that the axis goes straight to you from the origin of coordinates. Consider a function that continuous in each area point. The graph of this function is surface, and the small happiness is that in order to solve today's problem, we do not need to know what this surface looks like at all. It can be located above, below, cross the plane - all this is not important. And the following is important: according to Weierstrass theorems, continuous v limited closed area, the function reaches its maximum (of the "highest") and least (of the "lowest") values ​​to be found. These values ​​are achieved or v stationary points, belonging to the regionD , or at points that lie on the boundary of this region. From which follows a simple and transparent solution algorithm:

Example 1

In a limited enclosed area

Solution: First of all, you need to depict the area on the drawing. Unfortunately, it is technically difficult for me to make an interactive model of the problem, and therefore I will immediately give the final illustration, which shows all the "suspicious" points found during the study. Usually they are put down one after another as they are found:

Based on the preamble, the decision can be conveniently divided into two points:

I) Let's find stationary points. This is a standard action that we have repeatedly performed in the lesson. about extrema of several variables:

Found stationary point belongs areas: (mark it on the drawing), which means that we should calculate the value of the function at a given point:

- as in the article The largest and smallest values ​​of a function on a segment, I will highlight the important results in bold. In a notebook, it is convenient to circle them with a pencil.

Pay attention to our second happiness - there is no point in checking sufficient condition for an extremum. Why? Even if at the point the function reaches, for example, local minimum, then this DOES NOT MEAN that the resulting value will be minimal throughout the region (see the beginning of the lesson about unconditional extremes) .

What if the stationary point does NOT belong to the area? Almost nothing! It should be noted that and go to the next paragraph.

II) We investigate the border of the region.

Since the border consists of the sides of a triangle, it is convenient to divide the study into 3 subparagraphs. But it is better to do it not anyhow. From my point of view, at first it is more advantageous to consider segments parallel to the coordinate axes, and first of all, those lying on the axes themselves. To catch the whole sequence and logic of actions, try to study the ending "in one breath":

1) Let's deal with the lower side of the triangle. To do this, we substitute directly into the function:

Alternatively, you can do it like this:

Geometrically, this means that the coordinate plane (which is also given by the equation)"cut out" from surfaces"spatial" parabola, the top of which immediately falls under suspicion. Let's find out where is she:

- the resulting value "hit" in the area, and it may well be that at the point (mark on the drawing) the function reaches the largest or smallest value in the entire area. Anyway, let's do the calculations:

Other "candidates" are, of course, the ends of the segment. Calculate the values ​​of the function at points (mark on the drawing):

Here, by the way, you can perform an oral mini-check on the "stripped down" version:

2) To study the right side of the triangle, we substitute it into the function and “put things in order there”:

Here we immediately perform a rough check, “ringing” the already processed end of the segment:
, perfect.

The geometric situation is related to the previous point:

- the resulting value also “entered the scope of our interests”, which means that we need to calculate what the function is equal to at the point that has appeared:

Let's examine the second end of the segment:

Using the function , let's check:

3) Everyone probably knows how to explore the remaining side. We substitute into the function and carry out simplifications:

Line ends have already been investigated, but on the draft we still check whether we found the function correctly :
– coincided with the result of the 1st subparagraph;
– coincided with the result of the 2nd subparagraph.

It remains to find out if there is something interesting inside the segment :

- there is! Substituting a straight line into the equation, we get the ordinate of this “interestingness”:

We mark a point on the drawing and find the corresponding value of the function:

Let's control the calculations according to the "budget" version :
, order.

And the final step: CAREFULLY look through all the "fat" numbers, I recommend even beginners to make a single list:

from which we choose the largest and smallest values. Answer write in the style of the problem of finding the largest and smallest values ​​of the function on the interval:

Just in case, I will once again comment on the geometric meaning of the result:
– here is the highest point of the surface in the region ;
- here is the lowest point of the surface in the area.

In the analyzed problem, we found 7 “suspicious” points, but their number varies from task to task. For a triangular region, the minimum "exploration set" consists of three points. This happens when the function, for example, sets plane- it is quite clear that there are no stationary points, and the function can reach the maximum / minimum values ​​only at the vertices of the triangle. But there are no such examples once, twice - usually you have to deal with some kind of surface of the 2nd order.

If you solve such tasks a little, then triangles can make your head spin, and therefore I have prepared unusual examples for you to make it square :))

Example 2

Find the largest and smallest values ​​of a function in a closed area bounded by lines

Example 3

Find the largest and smallest values ​​of a function in a bounded closed area.

Pay special attention to the rational order and technique of studying the border of the area, as well as to the chain of intermediate checks, which will almost completely avoid computational errors. Generally speaking, you can solve it as you like, but in some problems, for example, in the same Example 2, there is every chance to significantly complicate your life. An approximate example of finishing assignments at the end of the lesson.

We systematize the solution algorithm, otherwise, with my diligence of a spider, it somehow got lost in a long thread of comments of the 1st example:

- At the first step, we build an area, it is desirable to shade it, and highlight the border with a thick line. During the solution, points will appear that need to be put on the drawing.

– Find stationary points and calculate the values ​​of the function only in those, which belong to the area . The obtained values ​​are highlighted in the text (for example, circled with a pencil). If the stationary point does NOT belong to the area, then we mark this fact with an icon or verbally. If there are no stationary points at all, then we draw a written conclusion that they are absent. In any case, this item cannot be skipped!

– Exploring the border area. First, it is advantageous to deal with straight lines that are parallel to the coordinate axes (if there are any). The function values ​​calculated at "suspicious" points are also highlighted. A lot has been said about the solution technique above and something else will be said below - read, re-read, delve into!

- From the selected numbers, select the largest and smallest values ​​\u200b\u200band give an answer. Sometimes it happens that the function reaches such values ​​at several points at once - in this case, all these points should be reflected in the answer. Let, for example, and it turned out that this is the smallest value. Then we write that

The final examples are devoted to other useful ideas that will come in handy in practice:

Example 4

Find the largest and smallest values ​​of a function in a closed area .

I have kept the author's formulation, in which the area is given as a double inequality. This condition can be written in an equivalent system or in a more traditional form for this problem:

I remind you that with non-linear we encountered inequalities on , and if you do not understand the geometric meaning of the entry, then please do not delay and clarify the situation right now ;-)

Solution, as always, begins with the construction of the area, which is a kind of "sole":

Hmm, sometimes you have to gnaw not only the granite of science ....

I) Find stationary points:

Idiot's dream system :)

The stationary point belongs to the region, namely, lies on its boundary.

And so, it’s nothing ... fun lesson went - that’s what it means to drink the right tea =)

II) We investigate the border of the region. Without further ado, let's start with the x-axis:

1) If , then

Find where the top of the parabola is:
- Appreciate such moments - "hit" right to the point, from which everything is already clear. But don't forget to check:

Let's calculate the values ​​of the function at the ends of the segment:

2) We will deal with the lower part of the “sole” “in one sitting” - without any complexes we substitute it into the function, moreover, we will only be interested in the segment:

Control:

Now this is already bringing some revival to the monotonous ride on a knurled track. Let's find the critical points:

We decide quadratic equation do you remember this one? ... However, remember, of course, otherwise you would not have read these lines =) If in the two previous examples calculations in decimal fractions were convenient (which, by the way, is rare), then here we are waiting for the usual ordinary fractions. We find the “x” roots and, using the equation, determine the corresponding “game” coordinates of the “candidate” points:


Let's calculate the values ​​of the function at the found points:

Check the function yourself.

Now we carefully study the won trophies and write down answer:

Here are the "candidates", so the "candidates"!

For a standalone solution:

Example 5

Find the smallest and largest values ​​of a function in a closed area

An entry with curly braces reads like this: “a set of points such that”.

Sometimes in such examples they use Lagrange multiplier method, but the real need to use it is unlikely to arise. So, for example, if a function with the same area "de" is given, then after substitution into it - with a derivative of no difficulties; moreover, everything is drawn up in a “one line” (with signs) without the need to consider the upper and lower semicircles separately. But, of course, there are more complicated cases, where without the Lagrange function (where , for example, is the same circle equation) it's hard to get by - how hard it is to get by without a good rest!

All the best to pass the session and see you soon next season!

Solutions and answers:

Example 2: Solution: draw the area on the drawing:

In this article I will talk about how to apply the ability to find to the study of a function: to find its largest or smallest value. And then we will solve several problems from Task B15 from the Open Task Bank for .

As usual, let's start with the theory first.

At the beginning of any study of a function, we find it

To find the largest or smallest value of the function, you need to investigate on which intervals the function increases and on which it decreases.

To do this, you need to find the derivative of the function and study its intervals of constant sign, that is, the intervals on which the derivative retains its sign.

The intervals on which the derivative of a function is positive are intervals of increasing function.

The intervals on which the derivative of a function is negative are intervals of decreasing function.

one . Let's solve task B15 (No. 245184)

To solve it, we will follow the following algorithm:

a) Find the domain of the function

b) Find the derivative of the function .

c) Set it equal to zero.

d) Let us find the intervals of constant sign of the function.

e) Find the point at which the function takes the greatest value.

f) Find the value of the function at this point.

I tell the detailed solution of this task in the VIDEO LESSON:

Probably your browser is not supported. To use the "Unified State Examination Hour" simulator, try downloading
Firefox

2. Let's solve task B15 (No. 282862)

Find the largest value of a function on the segment

It is obvious that the function takes the greatest value on the segment at the maximum point, at x=2. Find the value of the function at this point:

Answer: 5

3 . Let's solve task B15 (No. 245180):

Find the largest value of a function

1.title="(!LANG:ln5>0">, , т.к. title="5>1">, поэтому это число не влияет на знак неравенства.!}

2. Since the scope of the original function title="(!LANG:4-2x-x^2>0">, следовательно знаменатель дроби всегда больще нуля и дробь меняет знак только в нуле числителя.!}

3. The numerator is zero at . Let's check if the ODZ belongs to the function. To do this, check if the condition title="(!LANG:4-2x-x^2>0"> при .!}

Title="4-2(-1)-((-1))^2>0">,

so the point belongs to the ODZ of the function

We examine the sign of the derivative to the right and left of the point:

We see that the function takes the greatest value at the point . Now let's find the value of the function at :

Note 1. Note that in this problem we did not find the domain of the function: we only fixed the constraints and checked whether the point at which the derivative is equal to zero belongs to the domain of the function. In this problem, this turned out to be enough. However, this is not always the case. It depends on the task.

Remark 2. When studying the behavior of a complex function, one can use the following rule:

• if the outer function of a compound function is increasing, then the function takes on its greatest value at the same point at which the inner function takes on its greatest value. This follows from the definition of an increasing function: the function increases on the interval I if the larger value of the argument from this interval corresponds to the larger value of the function.
• if the outer function of a complex function is decreasing, then the function takes on the largest value at the same point at which the inner function takes on the smallest value . This follows from the definition of a decreasing function: the function decreases on the interval I if the larger value of the argument from this interval corresponds to the smaller value of the function

In our example, the outer function - increases over the entire domain of definition. Under the sign of the logarithm is an expression - a square trinomial, which, with a negative senior coefficient, takes the largest value at the point . Next, we substitute this value of x into the equation of the function and find its largest value.

What is an extremum of a function and what is the necessary condition for an extremum?

The extremum of a function is the maximum and minimum of the function.

The necessary condition for the maximum and minimum (extremum) of the function is as follows: if the function f(x) has an extremum at the point x = a, then at this point the derivative is either zero, or infinite, or does not exist.

This condition is necessary, but not sufficient. The derivative at the point x = a can vanish, go to infinity, or not exist without the function having an extremum at this point.

What is the sufficient condition for the extremum of the function (maximum or minimum)?

First condition:

If, in sufficient proximity to the point x = a, the derivative f?(x) is positive to the left of a and negative to the right of a, then at the point x = a itself, the function f(x) has maximum

If, in sufficient proximity to the point x = a, the derivative f?(x) is negative to the left of a and positive to the right of a, then at the point x = a itself, the function f(x) has minimum provided that the function f(x) is continuous here.

Instead, you can use the second sufficient condition for the extremum of the function:

Let at the point x = and the first derivative f? (x) vanishes; if the second derivative f??(а) is negative, then the function f(x) has a maximum at the point x = a, if it is positive, then a minimum.

What is the critical point of a function and how to find it?

This is the value of the function argument at which the function has an extremum (i.e. maximum or minimum). To find it, you need find the derivative function f?(x) and, equating it to zero, solve the equation f?(x) = 0. The roots of this equation, as well as those points at which the derivative of this function does not exist, are critical points, i.e., the values ​​of the argument at which there may be an extremum. They can be easily identified by looking at derivative graph: we are interested in those values ​​of the argument at which the graph of the function intersects the abscissa axis (Ox axis) and those at which the graph suffers breaks.

For example, let's find extremum of the parabola.

Function y(x) = 3x2 + 2x - 50.

Function derivative: y?(x) = 6x + 2

We solve the equation: y?(x) = 0

6x + 2 = 0, 6x = -2, x = -2/6 = -1/3

In this case, the critical point is x0=-1/3. It is for this value of the argument that the function has extremum. To get it find, we substitute the found number in the expression for the function instead of "x":

y0 = 3*(-1/3)2 + 2*(-1/3) - 50 = 3*1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50.333.

How to determine the maximum and minimum of a function, i.e. its largest and smallest values?

If the sign of the derivative changes from “plus” to “minus” when passing through the critical point x0, then x0 is maximum point; if the sign of the derivative changes from minus to plus, then x0 is minimum point; if the sign does not change, then at the point x0 there is neither a maximum nor a minimum.

For the considered example:

We take an arbitrary value of the argument to the left of the critical point: x = -1

When x = -1, the value of the derivative will be y? (-1) = 6 * (-1) + 2 = -6 + 2 = -4 (i.e., the minus sign).

Now we take an arbitrary value of the argument to the right of the critical point: x = 1

For x = 1, the value of the derivative will be y(1) = 6 * 1 + 2 = 6 + 2 = 8 (i.e., the plus sign).

As you can see, when passing through the critical point, the derivative changed sign from minus to plus. This means that at the critical value of x0 we have a minimum point.

The largest and smallest value of the function on the interval(on the segment) are found by the same procedure, only taking into account the fact that, perhaps, not all critical points will lie within the specified interval. Those critical points that are outside the interval must be excluded from consideration. If there is only one critical point inside the interval, it will either have a maximum or a minimum. In this case, to determine the largest and smallest values ​​of the function, we also take into account the values ​​of the function at the ends of the interval.

For example, let's find the largest and smallest values ​​of the function

y (x) \u003d 3 sin (x) - 0.5x

at intervals:

So the derivative of the function is

y?(x) = 3cos(x) - 0.5

We solve the equation 3cos(x) - 0.5 = 0

cos(x) = 0.5/3 = 0.16667

x \u003d ± arccos (0.16667) + 2πk.

We find critical points on the interval [-9; 9]:

x \u003d arccos (0.16667) - 2π * 2 \u003d -11.163 (not included in the interval)

x \u003d -arccos (0.16667) - 2π * 1 \u003d -7.687

x \u003d arccos (0.16667) - 2π * 1 \u003d -4.88

x \u003d -arccos (0.16667) + 2π * 0 \u003d -1.403

x \u003d arccos (0.16667) + 2π * 0 \u003d 1.403

x \u003d -arccos (0.16667) + 2π * 1 \u003d 4.88

x \u003d arccos (0.16667) + 2π * 1 \u003d 7.687

x \u003d -arccos (0.16667) + 2π * 2 \u003d 11.163 (not included in the interval)

We find the values ​​of the function at critical values ​​of the argument:

y(-7.687) = 3cos(-7.687) - 0.5 = 0.885

y(-4.88) = 3cos(-4.88) - 0.5 = 5.398

y(-1.403) = 3cos(-1.403) - 0.5 = -2.256

y(1.403) = 3cos(1.403) - 0.5 = 2.256

y(4.88) = 3cos(4.88) - 0.5 = -5.398

y(7.687) = 3cos(7.687) - 0.5 = -0.885

It can be seen that on the interval [-9; 9] the function has the greatest value at x = -4.88:

x = -4.88, y = 5.398,

and the smallest - at x = 4.88:

x = 4.88, y = -5.398.

On the interval [-6; -3] we have only one critical point: x = -4.88. The value of the function at x = -4.88 is y = 5.398.

We find the value of the function at the ends of the interval:

y(-6) = 3cos(-6) - 0.5 = 3.838

y(-3) = 3cos(-3) - 0.5 = 1.077

On the interval [-6; -3] we have the largest value of the function

y = 5.398 at x = -4.88

the smallest value is

y = 1.077 at x = -3

How to find the inflection points of a function graph and determine the sides of convexity and concavity?

To find all the inflection points of the line y \u003d f (x), you need to find the second derivative, equate it to zero (solve the equation) and test all those values ​​of x for which the second derivative is zero, infinite or does not exist. If, when passing through one of these values, the second derivative changes sign, then the graph of the function has an inflection at this point. If it does not change, then there is no inflection.

The roots of the equation f ? (x) = 0, as well as possible points of discontinuity of the function and the second derivative, divide the domain of the function into a number of intervals. The convexity at each of their intervals is determined by the sign of the second derivative. If the second derivative at a point on the interval under study is positive, then the line y = f(x) is concave upwards here, and if it is negative, then downwards.

How to find extrema of a function of two variables?

To find the extrema of the function f(x, y), differentiable in the area of ​​its assignment, you need:

1) find the critical points, and for this, solve the system of equations

fx? (x,y) = 0, fy? (x,y) = 0

2) for each critical point P0(a;b), investigate whether the sign of the difference remains unchanged

for all points (x; y) sufficiently close to P0. If the difference retains a positive sign, then at the point P0 we have a minimum, if negative, then a maximum. If the difference does not retain its sign, then there is no extremum at the point Р0.

Similarly, the extrema of the function are determined for a larger number of arguments.

Which non-alcoholic carbonated drinks clean surfaces
There is an opinion that the non-alcoholic carbonated drink Coca-Cola is able to dissolve meat. Unfortunately, there is no direct evidence for this. On the contrary, there are affirmative facts confirming that meat left in the Coca-Cola drink for two days changes in consumer properties and does not disappear anywhere.

Layouts of typical apartments, descriptions and photographs of houses can be found on the websites: - www.kvadroom.ru/planirovki - www.prime-realty.ru/tip/tip.htm - goodgoods.ru/pages/1093353787.html - www.cnko. net/art

How to treat neurosis
Neurosis (novolat. neurosis, comes from other Greek. νε?ρον - nerve; synonyms - psychoneurosis, neurotic disorder) - in the clinic: a collective name for a group of functional psychogenic reversible disorders that tend to

What is aphelion
The apocenter is the point in the orbit at which a body in an elliptical orbit around another body reaches its maximum distance from the latter. At the same point, according to Kepler's second law, the speed of orbital motion becomes minimal. The apocenter is located at a point diametrically opposite to the periapsis. In special cases, it is customary to use special terms:

What is mammon
Mamon (m. R.), mammon (f. R.) - a word derived from the Greek. mammonas and meaning wealth, earthly treasures, blessings. For some ancient pagan peoples, he was the god of wealth and profit. It is mentioned in Holy Scripture by the Evangelists Matthew and Luke: “No one can serve two masters: for either he will hate one, and the other

When is Orthodox Easter in 2049
In 2015, Orthodox Easter will be on April 12, and Catholic Easter on April 5. In church calendars, the dates of Orthodox Easter are given according to the Julian calendar (old style), while Catholic Easter is considered according to the modern Gregorian calendar (new style), so matching dates requires some mental effort

What is a ruble
The ruble is the name of the modern currencies of Russia, Belarus (Belarusian ruble), Transnistria (Pridnestrovian ruble). The Russian ruble also circulates in South Ossetia and Abkhazia. In the past - the monetary unit of the Russian republics and principalities, the Grand Duchy of Moscow, the Russian kingdom, the Grand Duchy of Lithuania, the Russian Empire and various

How long was Ariel Sharon in a coma
Ariel Arik Sharon (Sheinerman) - Israeli military, political and statesman, Prime Minister of Israel in 2001 - 2006. Date of birth: February 26, 1928 Place of birth: Kfar Malal settlement near Kfar Saba, Israel Date of death: January 11, 2014 Place of death: Ramat Gan, Gush Dan, Iz

Who were the Neanderthals
Neanderthal man, Neanderthal man (lat. Homo neanderthalensis or Homo sapiens neanderthalensis) is a fossil species of people who lived 300-24 thousand years ago. Origin of the name It is believed that the Neanderthal skull was first found in 1856.

How old is Geoffrey Rush
Geoffrey Rush is an Australian film and theater actor. Winner of Oscar (1997), BAFTA (1996, 1999), Golden Globe (1997, 2005). The most famous films with his participation - "Shine"

How to determine the intervals of convexity and concavity of a function graph
What is an extremum of a function and what is the necessary condition for an extremum? The extremum of a function is the maximum and minimum of the function. The necessary condition for the maximum and minimum (extremum) of the function is as follows: if the function f(x) has an extremum at the point x = a, then at this point the derivative is either zero, or infinite, or does not exist. This condition is necessary, but not sufficient. Derivative in t

Let the function y=f(X) continuous on the interval [ a, b]. As is known, such a function reaches its maximum and minimum values ​​on this interval. The function can take these values ​​either at an interior point of the segment [ a, b], or on the boundary of the segment.

To find the largest and smallest values ​​of a function on the segment [ a, b] necessary:

1) find the critical points of the function in the interval ( a, b);

2) calculate the values ​​of the function at the found critical points;

3) calculate the values ​​of the function at the ends of the segment, that is, for x=a and x = b;

4) from all the calculated values ​​of the function, choose the largest and smallest.

Example. Find the largest and smallest values ​​of a function

on the segment.

Finding critical points:

These points lie inside the segment ; y(1) = ‒ 3; y(2) = ‒ 4; y(0) = ‒ 8; y(3) = 1;

at the point x= 3 and at the point x= 0.

Investigation of a function for convexity and an inflection point.

Function y = f (x) called convexup in between (a, b) , if its graph lies under a tangent drawn at any point of this interval, and is called convex down (concave) if its graph lies above the tangent.

The point at the transition through which the convexity is replaced by concavity or vice versa is called inflection point.

Algorithm for studying for convexity and inflection point:

1. Find the critical points of the second kind, that is, the points at which the second derivative is equal to zero or does not exist.

2. Put critical points on the number line, breaking it into intervals. Find the sign of the second derivative on each interval; if , then the function is convex upwards, if, then the function is convex downwards.

3. If, when passing through a critical point of the second kind, it changes sign and at this point the second derivative is equal to zero, then this point is the abscissa of the inflection point. Find its ordinate.

Asymptotes of the graph of a function. Investigation of a function into asymptotes.

Definition. The asymptote of the graph of a function is called straight, which has the property that the distance from any point of the graph to this line tends to zero with an unlimited removal of the graph point from the origin.

There are three types of asymptotes: vertical, horizontal and inclined.

Definition. Direct called vertical asymptote function graph y = f(x), if at least one of the one-sided limits of the function at this point is equal to infinity, that is

where is the discontinuity point of the function, that is, it does not belong to the domain of definition.

Example.

D( y) = (‒ ∞; 2) (2; + ∞)

x= 2 - breaking point.

Definition. Straight y=A called horizontal asymptote function graph y = f(x) at , if

Example.

Definition. Straight y=kx +b (k≠ 0) is called oblique asymptote function graph y = f(x) at , where

General scheme for the study of functions and plotting.

Function research algorithmy = f(x) :

1. Find the domain of the function D (y).

2. Find (if possible) the points of intersection of the graph with the coordinate axes (with x= 0 and at y = 0).

3. Investigate for even and odd functions ( y (‒ x) = y (x) ‒ parity; y(‒ x) = ‒ y (x) ‒ odd).

4. Find the asymptotes of the graph of the function.

5. Find intervals of monotonicity of the function.

6. Find the extrema of the function.

7. Find the intervals of convexity (concavity) and inflection points of the graph of the function.

8. On the basis of the conducted research, construct a graph of the function.

Example. Investigate the function and plot its graph.

1) D (y) =

x= 4 - breaking point.

2) When x = 0,

(0; – 5) – point of intersection with oy.

At y = 0,

3) y(‒ x)= general function (neither even nor odd).

4) We investigate for asymptotes.

a) vertical

b) horizontal

c) find oblique asymptotes where

‒oblique asymptote equation

5) In this equation, it is not required to find intervals of monotonicity of the function.

6)

These critical points partition the entire domain of the function on the interval (˗∞; ˗2), (˗2; 4), (4; 10) and (10; +∞). It is convenient to present the obtained results in the form of the following table.

The process of finding the smallest and largest values ​​of a function on a segment is reminiscent of a fascinating flight around an object (a graph of a function) on a helicopter with firing from a long-range cannon at certain points and choosing from these points very special points for control shots. Points are selected in a certain way and according to certain rules. By what rules? We will talk about this further.

If the function y = f(x) continuous on the interval [ a, b] , then it reaches on this segment least and highest values . This can either happen in extremum points or at the ends of the segment. Therefore, to find least and the largest values ​​of the function , continuous on the segment [ a, b] , you need to calculate its values ​​in all critical points and at the ends of the segment, and then choose the smallest and largest of them.

Let, for example, it is required to determine the maximum value of the function f(x) on the segment [ a, b] . To do this, find all its critical points lying on [ a, b] .

critical point is called the point at which function defined, and her derivative is either zero or does not exist. Then you should calculate the values ​​of the function at critical points. And, finally, one should compare the values ​​of the function at critical points and at the ends of the segment ( f(a) and f(b) ). The largest of these numbers will be the largest value of the function on the segment [a, b] .

The problem of finding the smallest values ​​of the function .

We are looking for the smallest and largest values ​​​​of the function together

Example 1. Find the smallest and largest values ​​of a function on the segment [-1, 2] .

Solution. We find the derivative of this function. Equate the derivative to zero () and get two critical points: and . To find the smallest and largest values ​​of a function on a given segment, it is enough to calculate its values ​​at the ends of the segment and at the point , since the point does not belong to the segment [-1, 2] . These function values ​​are the following: , , . It follows that smallest function value(marked in red on the graph below), equal to -7, is reached at the right end of the segment - at the point , and greatest(also red on the graph), is equal to 9, - at the critical point .

If the function is continuous in a certain interval and this interval is not a segment (but is, for example, an interval; the difference between an interval and a segment: the boundary points of the interval are not included in the interval, but the boundary points of the segment are included in the segment), then among the values ​​of the function there may not be be the smallest and largest. So, for example, the function depicted in the figure below is continuous on ]-∞, +∞[ and does not have the largest value.

However, for any interval (closed, open, or infinite), the following property of continuous functions holds.

Example 4. Find the smallest and largest values ​​of a function on the segment [-1, 3] .

Solution. We find the derivative of this function as the derivative of the quotient:

.

We equate the derivative to zero, which gives us one critical point: . It belongs to the interval [-1, 3] . To find the smallest and largest values ​​of a function on a given segment, we find its values ​​at the ends of the segment and at the found critical point:

Let's compare these values. Conclusion: equal to -5/13, at the point and the greatest value equal to 1 at the point .

We continue to search for the smallest and largest values ​​​​of the function together

There are teachers who, on the topic of finding the smallest and largest values ​​of a function, do not give students examples more complicated than those just considered, that is, those in which the function is a polynomial or a fraction, the numerator and denominator of which are polynomials. But we will not limit ourselves to such examples, since among teachers there are lovers of making students think in full (table of derivatives). Therefore, the logarithm and the trigonometric function will be used.

Example 6. Find the smallest and largest values ​​of a function on the segment .

Solution. We find the derivative of this function as derivative of the product :

We equate the derivative to zero, which gives one critical point: . It belongs to the segment. To find the smallest and largest values ​​of a function on a given segment, we find its values ​​at the ends of the segment and at the found critical point:

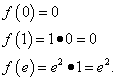
The result of all actions: the function reaches its minimum value, equal to 0, at a point and at a point and the greatest value equal to e² , at the point .

Example 7. Find the smallest and largest values ​​of a function on the segment .

Solution. We find the derivative of this function:

Equate the derivative to zero:

The only critical point belongs to the segment . To find the smallest and largest values ​​of a function on a given segment, we find its values ​​at the ends of the segment and at the found critical point:

Conclusion: the function reaches its minimum value, equal to , at the point and the greatest value, equal to , at the point .

In applied extremal problems, finding the smallest (largest) function values, as a rule, is reduced to finding the minimum (maximum). But it is not the minima or maxima themselves that are of greater practical interest, but the values ​​of the argument at which they are achieved. When solving applied problems, an additional difficulty arises - the compilation of functions that describe the phenomenon or process under consideration.

Example 8 A tank with a capacity of 4, having the shape of a parallelepiped with a square base and open at the top, must be tinned. What should be the dimensions of the tank in order to cover it with the least amount of material?

Solution. Let x- base side h- tank height, S- its surface area without cover, V- its volume. The surface area of ​​the tank is expressed by the formula , i.e. is a function of two variables. To express S as a function of one variable, we use the fact that , whence . Substituting the found expression h into the formula for S:

Let us examine this function for an extremum. It is defined and differentiable everywhere in ]0, +∞[ , and

.

We equate the derivative to zero () and find the critical point. In addition, when the derivative does not exist, but this value is not included in the domain of definition and therefore cannot be an extremum point. So, - the only critical point. Let's check it for the presence of an extremum using the second sufficient sign. Let's find the second derivative. When the second derivative is greater than zero (). This means that when the function reaches a minimum . Because this minimum - the only extremum of this function, it is its smallest value. So, the side of the base of the tank should be equal to 2 m, and its height.

Example 9 From paragraph A, located on the railway line, to the point WITH, at a distance from it l, goods must be transported. The cost of transporting a weight unit per unit distance by rail is equal to , and by highway it is equal to . To what point M railroad line should be held highway to transport cargo from A v WITH was the most economical AB railroad is assumed to be straight)?